题目内容
在一个棱长为6的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,则正方体的棱长的最大值为分析:在一个棱长为6的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,说明正方体在正四面体的内切球内,求出内切球的直径,就是正方体的对角线的长,然后求出正方体的棱长.
解答:解:设球的半径为r,由正四面体的体积得:4×
×r×
×62=
×
×62×
,所以r=
,
设正方体的最大棱长为a,所以,3a2=(
)2,a=
故答案为:
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| ||
| 4 |
62-(
|
| ||
| 2 |
设正方体的最大棱长为a,所以,3a2=(
| 6 |
| 2 |
故答案为:
| 2 |
点评:本题是中档题,考查正四面体的内接球的知识,球的内接正方体的棱长的求法,考查空间想象能力,转化思想,计算能力.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
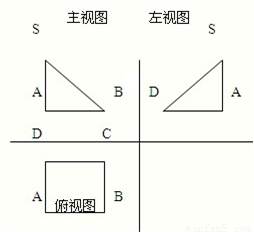
 已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值. 已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.