题目内容
已知F为抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|最小值为8.
(1)求该抛物线的方程;
(2)若直线x-y-3=0与抛物线交于B、C两点,求△BFC的面积.
(1)求该抛物线的方程;
(2)若直线x-y-3=0与抛物线交于B、C两点,求△BFC的面积.
分析:(1)利用抛物线的定义和三点共线时的性质即可求出;
(2)利用弦长公式和点到直线的距离公式即可得出.
(2)利用弦长公式和点到直线的距离公式即可得出.
解答:解:(1)设d为点P到x=-
的距离,则由抛物线定义,|PF|=d,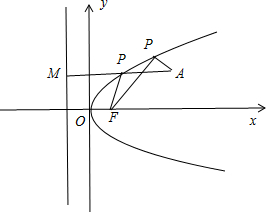
∴当点P为过点A且垂直于准线的直线与抛物线的交点时,|PA|+|PF|取得最小值,即4+
=8,解得p=8.
∴抛物线的方程为y2=16x.
(2)设B(x1,y1),C(x2,y2),联立
得y2-16y-48=0,
显然△>0,y1+y2=16,y1y2=-48.
∴|y1-y2|=
=
=8
,
∴|BC|=
|y1-y2|=8
.
又∵F(4,0)到直线l的距离为
=
,
∴S△BFC=
|BC|•d=
×8
×
=4
.
| p |
| 2 |

∴当点P为过点A且垂直于准线的直线与抛物线的交点时,|PA|+|PF|取得最小值,即4+
| p |
| 2 |
∴抛物线的方程为y2=16x.
(2)设B(x1,y1),C(x2,y2),联立
|
显然△>0,y1+y2=16,y1y2=-48.
∴|y1-y2|=
| (y1+y2)2-4y1y2 |
| 162+4×48 |
| 7 |
∴|BC|=
| 2 |
| 14 |
又∵F(4,0)到直线l的距离为
| |4-3| | ||
|
| ||
| 2 |
∴S△BFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 14 |
| ||
| 2 |
| 7 |
点评:熟练掌握抛物线的定义、两线段长的和取得最小值的条件、直线与圆锥曲线相交时的弦长公式、点到直线的距离公式是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目