题目内容
作函数y＝|log2(x＋1)|＋2的图象．
答案：
解析：
提示：
解析：
|
解：第一步：作y＝log2x的图象(图甲)． 第二步：将y＝log2x的图象沿x轴向左平移1个单位，得y＝log(x＋1)的图象(图乙)． 第三步：将y＝log2(1＋x)在x轴下方的图象作关于x轴的对称变换，得y＝|log2(x＋1)|的图象(图丙)． 第四步：将y＝|log2(x＋1)|的图象，沿y轴方向向上平移2个单位，便得到所求函数的图象(图丁)．
思想方法小结：一般地，函数y＝f(x－a)＋b(a，b为实数)的图象，是由函数y＝f(x)的图象沿x轴向右(或向左)平移|a|个单位，(此时为f(x－a)的图象)，再沿y轴向上(或向下)平移|b|个单位而得． 含有绝对值的函数的图象是一种对称变换，一般地，y＝f(|x－a|)的图象是关于直线x＝a对称的轴对称图形；函数y＝|f(x)|的图象与y＝f(x)的图象，在f(x)≥0时相同，而在f(x)＜0时，关于x轴对称． |
提示：
|
作复合函数的图象时，可先作它的基本函数的图象，然后适当的交换，分步骤完成． |
练习册系列答案
相关题目
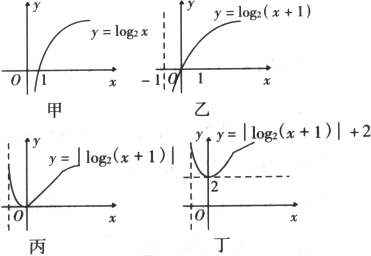
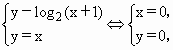所以点(0，0)在函数y＝log2(x＋1)的图象上，(0，0)点关于y＝x的对称的点还是其本身．函数y＝2x的图象向左或向右或向上平行移动都不会过(0，0)点，因此只能向下平行移动1个单位．
的简图，并写出函数的单调区间．