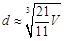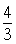题目内容
一个体积为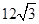
的正三棱柱的三视图，如图所示，则此正三棱柱的侧视图面积为（ ） 
A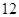． | B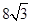． | C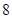． | D． |
D
解析试题分析：此几何体是一个正三棱柱，正视图即内侧面，底面正三角形的高是 2 
，由正三角形的性质可以求出其边长，由于本题中体积已知，故可设出棱柱的高，利用体积公式建立起关于高的方程求高，再由正方形的面积公式求侧视图的面积即可．解：设棱柱的高为h，由左视图知，底面正三角形的高是 2，由正三角形的性质知，其边长是4，故底面三角形的面积是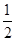
×2× 4="4" 由于其体积为 12，故有h×4=12，得h=3，由三视图的定义知，侧视图的宽即此三棱柱的高，故侧视图的宽是3，其面积为3×2=6，故选D
考点：简单空间图形的三视图
点评：本题考点是简单空间图形的三视图，考查根据作三视图的规则几何体的直观图的能力以及利用体积公式建立方程求参数的能力，三视图的投影规则是：“主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等”．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
，则这个圆锥的全面积是（ ）
四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯，如图所示．盛满酒后他们约定：先各自饮杯中酒的一半．设剩余酒的高度从左到右依次为h1，h2，h3，h4，则它们的大小关系正确的是（ ）
| A．h2＞h1＞h4 | B．h1＞h2＞h3 | C．h3＞h2＞h4 | D．h2＞h4＞h1 |
已知某几何体的三视图如图所示，那么这个几何体是( )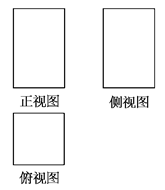
| A．长方体 | B．圆柱 | C．四棱锥 | D．四棱台 |
已知某几何体的三视图如图，其中正(主)视图中半圆的半径为1，则该几何体的体积为（ ）
A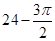． | B． | C． | D． |
,求其直径
的一个近似公式
. 人们还用过一些类似的近似公式. 根据
判断,下列近似公式中最精确的一个是（ ）
