题目内容
若递增的一次函数f（x）满足f[f（x）]=4x+3，则f（x）= ．
【答案】分析：利用待定系数法求一次函数的解析式．
解答：解：设一次函数的方程为f（x）=ax+b，因为一次函数为递增函数，所以a＞0．
则由f[f（x）]=4x+3，得f[ax+b]=a（ax+b）+b=a2x+ab+b=4x+3，
即
，解得
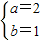，即f（x）=2x+1．
故答案为：2x+1
点评：本题主要考查利用待定系数法求一次函数的解析式，比较基础．
解答：解：设一次函数的方程为f（x）=ax+b，因为一次函数为递增函数，所以a＞0．
则由f[f（x）]=4x+3，得f[ax+b]=a（ax+b）+b=a2x+ab+b=4x+3，
即
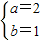，解得，即f（x）=2x+1．故答案为：2x+1
点评：本题主要考查利用待定系数法求一次函数的解析式，比较基础．
练习册系列答案
阅读快车系列答案
相关题目