题目内容
在三角形ABC中,有命题:①
-
=
;②
+
+
=
.③若(
+
).(
-
)=0,则三角形ABC为等腰三角形;④若
.
>0则三角形ABC为锐角三角形,上述命题正确的是
| AB |
| AC |
| BC |
| AB |
| BC |
| CA |
| 0 |
| AB |
| AC |
| AB |
| AC |
| AC |
| AB |
②③
②③
.分析:根据两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,判断各个选项是否正确.
解答:解:在三角形ABC中,由于
-
=
,故①不正确.
由于
+
+
=
+
=
,故②正确.
由于(
+
)•(
-
)=
2-
2=0,故有AB=AC,三角形ABC为等腰三角形,故③正确.
由于
•
=|
|•|
|cosA>0,故A为锐角,但B和C的范围不确定,故不能推出三角形ABC为锐角三角形,故④不正确.
故答案为 ②③.
| AB |
| AC |
| CB |
由于
| AB |
| BC |
| CA |
| AC |
| CA |
| 0 |
由于(
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
由于
| AB |
| AC |
| AB |
| AC |
故答案为 ②③.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
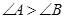 ,则
,则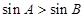 ;(2)若
;(2)若 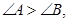 则
则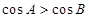 ;
;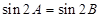 ,则A=B; (4) 若
,则A=B; (4) 若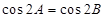 ,则A=B
,则A=B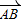 -
-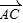 =
=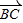 ;②
;②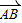 +
+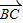 +
+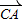 =
=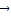 .③若(
.③若(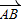 +
+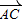 ).(
).( 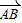 -
-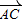 )=0,则三角形ABC为等腰三角形;④若
)=0,则三角形ABC为等腰三角形;④若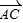 .
.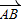 >0则三角形ABC为锐角三角形,上述命题正确的是 .
>0则三角形ABC为锐角三角形,上述命题正确的是 .