题目内容

对于抛物线y2=2px(p＞0),F为其焦点,过点F的直线l与抛物线交于A(x1,y1)、B(x2,y2)两点.

(1)求弦AB的长(用x1、x2、p表示);

(2)当AB⊥x轴时,求AB的长;

(3)判断以AB为直径的圆与抛物线的准线l的位置关系.

解析:(1)由定义知,|AF|、|BF|分别等于点A、B到准线x=-的距离,

∴|AF|=x1+,|BF|=x2+,则|AB|=|AF|+|BF|=x1+x2+p.

(2)当AB⊥x轴时,其方程为x=p,代入y2=2px,得y1=p,y2=-p,∴|AB|=2p,又称为抛物线的通径.

(3)如下图,设AB中点为M,分别过点A、B、M作准线的垂线,垂足为A1、B1、N,

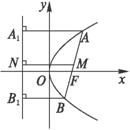
∵|MN|=(|A1A|+|B1B|)=(|AF|+|BF|)=|AB|,∴以AB为直径的圆与抛物线的准线l相切.


练习册系列答案
相关题目
已知动点M到定点F（1，0）的距离比M到定直线x=-2的距离小1．
（1）求证：M点的轨迹是抛物线，并求出其方程；
（2）我们知道：“过圆上任意一点P，任意作互相垂直的弦PA、PB，则弦AB必过圆心”（定点）．受此启发，研究下面问题：
对于抛物线y2=2px（p＞0）上某一定点P（非顶点），过P任意作互相垂直的弦PA、PB，弦AB是否经过定点？
（2013•松江区二模）已知双曲线C的中心在原点，D（1，0）是它的一个顶点，
d
=(1，
2
)是它的一条渐近线的一个方向向量．
（1）求双曲线C的方程；
（2）若过点（-3，0）任意作一条直线与双曲线C交于A，B两点 （A，B都不同于点D），求证：
DA
•
DB
为定值；
（3）对于双曲线Γ：
x2
a2
-
y2
b2
=1(a＞0，b＞0，a≠b)，E为它的右顶点，M，N为双曲线Γ上的两点（都不同于点E），且EM⊥EN，那么直线MN是否过定点？若是，请求出此定点的坐标；若不是，说明理由．然后在以下三个情形中选择一个，写出类似结论（不要求书写求解或证明过程）．
情形一：双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0，a≠b)及它的左顶点；
情形二：抛物线y2=2px（p＞0）及它的顶点；
情形三：椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)及它的顶点．

对于抛物线y2=2px(p>0),F为其焦点,过点F的直线l与抛物线交于A(x1,y1)、B(x2,y2)两点.

(1)求弦AB的长(用x1、x2、p表示);

(2)当AB⊥x轴时,求AB的长;

(3)判断以AB为直径的圆与抛物线的准线l的位置关系.
已知动点M到定点F（1，0）的距离比M到定直线x=-2的距离小1．
（1）求证：M点的轨迹是抛物线，并求出其方程；
（2）我们知道：“过圆上任意一点P，任意作互相垂直的弦PA、PB，则弦AB必过圆心”（定点）．受此启发，研究下面问题：
对于抛物线y2=2px（p＞0）上某一定点P（非顶点），过P任意作互相垂直的弦PA、PB，弦AB是否经过定点？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网