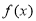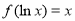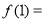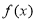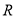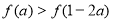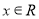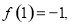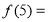题目内容
已知函数f(x)=loga(x+1)-loga(1-x)(a>0,a≠1)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性,并给出证明;
(3)当a>1时,求使f(x)>0的x的取值范围
(1) ;(2)
;(2) 为奇函数,证明见试题解析;(3)
为奇函数,证明见试题解析;(3) -=
-=
【解析】
试题分析:(1)函数的定义域是使函数式有意义的自变量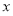 的取值集合,即
的取值集合,即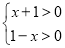 ,(2)判断奇偶性,可以直接用奇偶性的定义,证明
,(2)判断奇偶性,可以直接用奇偶性的定义,证明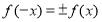 ,当然也可以通过证明
,当然也可以通过证明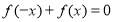
 来说明
来说明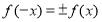 ;(3)利用对数函数的性质,
;(3)利用对数函数的性质,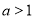 时,
时,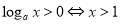
试题解析:(1)因为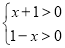 所以-1<x<1,所以f(x)的定义域为(-1,1) 5分
所以-1<x<1,所以f(x)的定义域为(-1,1) 5分
(2)f(x)为奇函数 因为f(x)定义域为(-1,1),且f(-x)=loga(-x+1)-loga(1+x)=-f(x),
所以f(x)为奇函数 10分
(3)因为当a>1时,f(x)在(-1,1)上单调递增,所以f(x)>0? >1,解得0<x<1
>1,解得0<x<1
所以使f(x)>0的x的取值范围是(0,1) 16分
考点:(1)函数的定义域;(2)函数的奇偶性;(3)对数函数的性质

练习册系列答案
相关题目