题目内容
设全集I=R,已知集合M={x|x2-10x+24<0},N={x|x2-2x-15≤0}.(1)求(∁IM)∩N;
(2)记集合A=(∁IM)∩N,已知集合B={x|a-1≤x≤5-a,a∈R},若A∪B=A,求实数a的取值范围.
【答案】分析:(1)先将M,N化简,求出∁IM,再计算得出最后结果.
(2)由A∪B=A,得出集合B是集合A的子集,然后根据集合端点值的关系列式求出a的范围.
解答:解:(1)M={x|x2-10x+24<0}={x|4<x<6},N={x|x2-2x-15≤0}={x|-3≤x≤5}.
∵全集I=R,∴∁IM={x|x≤4或x≥6}.
∴(∁IM)∩N={x|-3≤x≤4}.
(2)因为A∪B=A,所以B⊆A,
又A={x|-3≤x≤4},B={x|a-1≤x≤5-a},
∴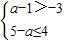
解得a≥1,符合题意,
符合条件的a的取值范围为[1,+∞).
点评:本题考查集合的混合运算,解一元二次不等式等.解答此题的关键是由A∪B=A得出集合A和B的关系,此题是基础题.
(2)由A∪B=A,得出集合B是集合A的子集,然后根据集合端点值的关系列式求出a的范围.
解答:解:(1)M={x|x2-10x+24<0}={x|4<x<6},N={x|x2-2x-15≤0}={x|-3≤x≤5}.
∵全集I=R,∴∁IM={x|x≤4或x≥6}.
∴(∁IM)∩N={x|-3≤x≤4}.
(2)因为A∪B=A,所以B⊆A,
又A={x|-3≤x≤4},B={x|a-1≤x≤5-a},
∴
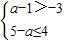
解得a≥1,符合题意,
符合条件的a的取值范围为[1,+∞).
点评:本题考查集合的混合运算,解一元二次不等式等.解答此题的关键是由A∪B=A得出集合A和B的关系,此题是基础题.

练习册系列答案
相关题目