题目内容
已知动圆P过点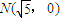 并且与圆
并且与圆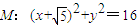 相外切,动圆圆心P的轨迹为W,轨迹W与x轴的交点为D.
相外切,动圆圆心P的轨迹为W,轨迹W与x轴的交点为D.(Ⅰ)求轨迹W的方程;
(Ⅱ)设直线l过点(m,0)(m>2)且与轨迹W有两个不同的交点A,B,求直线l斜率k的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若
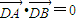 ,证明直线l过定点,并求出这个定点的坐标.
,证明直线l过定点,并求出这个定点的坐标.
【答案】分析:(1)由题意可知|PM|-|PN|=4由双曲线的定义可知W是以M,N为焦点的双曲线的右支,则曲线方程可得.
(2)设出直线l的方程,与双曲线方程联立消去y,设A(x1,y1).B(x2,y2),根据韦达定理表示出x1+x2和x1x2,x1,x2和判别式确定k的范围.
(3)利用A,B的坐标表示出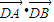 ,根据结果为0整理求得m,则直线的方程可得,根据直线方程可知直线l过定点,定点坐标为
,根据结果为0整理求得m,则直线的方程可得,根据直线方程可知直线l过定点,定点坐标为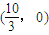 .
.
解答:解:(Ⅰ)由已知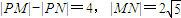 ,
,
∴点P的轨迹是以M,N为焦点的双曲线的右支,且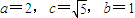 .
.
∴轨迹W的方程为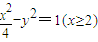 .
.
(Ⅱ)设直线l的方程为y=k(x-m)(m>2,k≠0).
由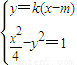 得(1-4k2)x2+8k2mx-4k2m-4=0.
得(1-4k2)x2+8k2mx-4k2m-4=0.
设A(x1,y1).B(x2,y2),
则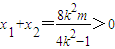 ,①
,①
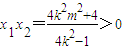 ,②
,②
△=64k4m2+4(1-4k2)(4k2m2+4)>0.③
由①②③得4k2>1.
∴直线l斜率k的取值范围是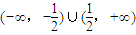 .
.
(Ⅲ) =(x1-2,y1)•(x2-2,y2)
=(x1-2,y1)•(x2-2,y2)
=(x1-2)(x2-2)+y1y2=x1x2-2(x1+x2)+4+k(x1-m)k(x2-m)
=(1+k2)x1x2-(2+mk2)(x1+x2)+4+k2m2
=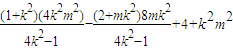 .
.
∵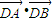 =0,
=0,
∴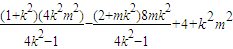 =0,
=0,
∴(1+k2)(4k2m2)-(2+mk2)8mk2+(4+k2m2)(4k2-1)=0,
∴20k2-16k2m+3k2m2=0.
∵k≠0,
∴3m2-16m+20=0,解得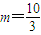 ,或m=2(舍).
,或m=2(舍).
∴直线l的方程为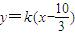 .
.
∴直线l过定点,定点坐标为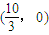 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和基本的运算能力.
(2)设出直线l的方程,与双曲线方程联立消去y,设A(x1,y1).B(x2,y2),根据韦达定理表示出x1+x2和x1x2,x1,x2和判别式确定k的范围.
(3)利用A,B的坐标表示出
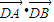 ,根据结果为0整理求得m,则直线的方程可得,根据直线方程可知直线l过定点,定点坐标为
,根据结果为0整理求得m,则直线的方程可得,根据直线方程可知直线l过定点,定点坐标为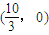 .
.解答:解:(Ⅰ)由已知
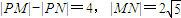 ,
,∴点P的轨迹是以M,N为焦点的双曲线的右支,且
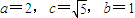 .
.∴轨迹W的方程为
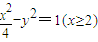 .
.(Ⅱ)设直线l的方程为y=k(x-m)(m>2,k≠0).
由
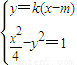 得(1-4k2)x2+8k2mx-4k2m-4=0.
得(1-4k2)x2+8k2mx-4k2m-4=0.设A(x1,y1).B(x2,y2),
则
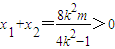 ,①
,①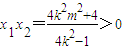 ,②
,②△=64k4m2+4(1-4k2)(4k2m2+4)>0.③
由①②③得4k2>1.
∴直线l斜率k的取值范围是
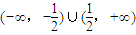 .
.(Ⅲ)
 =(x1-2,y1)•(x2-2,y2)
=(x1-2,y1)•(x2-2,y2)=(x1-2)(x2-2)+y1y2=x1x2-2(x1+x2)+4+k(x1-m)k(x2-m)
=(1+k2)x1x2-(2+mk2)(x1+x2)+4+k2m2
=
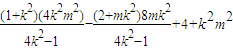 .
.∵
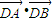 =0,
=0,∴
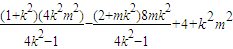 =0,
=0,∴(1+k2)(4k2m2)-(2+mk2)8mk2+(4+k2m2)(4k2-1)=0,
∴20k2-16k2m+3k2m2=0.
∵k≠0,
∴3m2-16m+20=0,解得
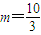 ,或m=2(舍).
,或m=2(舍).∴直线l的方程为
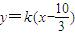 .
.∴直线l过定点,定点坐标为
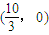 .
.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
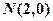 并且与圆
并且与圆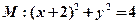 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线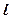 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。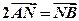 ,求直线
,求直线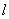 的方程;
的方程;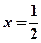 上是否存在一点Q,使得
上是否存在一点Q,使得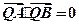 ,并说明理由。
,并说明理由。