题目内容
已知动圆P过点N(
，0)并且与圆M：(x+
)2+y2=16相外切，动圆圆心P的轨迹为W，轨迹W与x轴的交点为D．
（Ⅰ）求轨迹W的方程；
（Ⅱ）设直线l过点（m，0）（m＞2）且与轨迹W有两个不同的交点A，B，求直线l斜率k的取值范围；
（Ⅲ）在（Ⅱ）的条件下，若
•
=0，证明直线l过定点，并求出这个定点的坐标．
| 5 |
| 5 |
（Ⅰ）求轨迹W的方程；
（Ⅱ）设直线l过点（m，0）（m＞2）且与轨迹W有两个不同的交点A，B，求直线l斜率k的取值范围；
（Ⅲ）在（Ⅱ）的条件下，若
| DA |
| DB |
（Ⅰ）由已知|PM|-|PN|=4，|MN|=2
，
∴点P的轨迹是以M，N为焦点的双曲线的右支，且a=2，c=
，b=1．
∴轨迹W的方程为
-y2=1(x≥2)．
（Ⅱ）设直线l的方程为y=k（x-m）（m＞2，k≠0）．
由
得（1-4k2）x2+8k2mx-4k2m-4=0．
设A（x1，y1）．B（x2，y2），
则x1+x2=
＞0，①
x1x2=
＞0，②
△=64k4m2+4（1-4k2）（4k2m2+4）＞0．③
由①②③得4k2＞1．
∴直线l斜率k的取值范围是(-∞，-
)∪(
，+∞)．
（Ⅲ）
•
=（x1-2，y1）•（x2-2，y2）
=（x1-2）（x2-2）+y1y2=x1x2-2（x1+x2）+4+k（x1-m）k（x2-m）
=（1+k2）x1x2-（2+mk2）（x1+x2）+4+k2m2
=
-
+4+k2m2．
∵
•
=0，
∴
-
+4+k2m2=0，
∴（1+k2）（4k2m2）-（2+mk2）8mk2+（4+k2m2）（4k2-1）=0，
∴20k2-16k2m+3k2m2=0．
∵k≠0，
∴3m2-16m+20=0，解得m=
，或m=2（舍）．
∴直线l的方程为y=k(x-
)．
∴直线l过定点，定点坐标为(
，0)．
| 5 |
∴点P的轨迹是以M，N为焦点的双曲线的右支，且a=2，c=
| 5 |
∴轨迹W的方程为
| x2 |
| 4 |
（Ⅱ）设直线l的方程为y=k（x-m）（m＞2，k≠0）．
由
|
设A（x1，y1）．B（x2，y2），
则x1+x2=
| 8k2m |
| 4k2-1 |
x1x2=
| 4k2m2+4 |
| 4k2-1 |
△=64k4m2+4（1-4k2）（4k2m2+4）＞0．③
由①②③得4k2＞1．
∴直线l斜率k的取值范围是(-∞，-
| 1 |
| 2 |
| 1 |
| 2 |
（Ⅲ）
| DA |
| DB |
=（x1-2）（x2-2）+y1y2=x1x2-2（x1+x2）+4+k（x1-m）k（x2-m）
=（1+k2）x1x2-（2+mk2）（x1+x2）+4+k2m2
=
| (1+k2)(4k2m2) |
| 4k2-1 |
| (2+mk2)8mk2 |
| 4k2-1 |
∵
| DA |
| DB |
∴
| (1+k2)(4k2m2) |
| 4k2-1 |
| (2+mk2)8mk2 |
| 4k2-1 |
∴（1+k2）（4k2m2）-（2+mk2）8mk2+（4+k2m2）（4k2-1）=0，
∴20k2-16k2m+3k2m2=0．
∵k≠0，
∴3m2-16m+20=0，解得m=
| 10 |
| 3 |
∴直线l的方程为y=k(x-
| 10 |
| 3 |
∴直线l过定点，定点坐标为(
| 10 |
| 3 |
练习册系列答案
相关题目
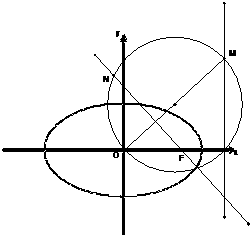（2011•石景山区一模）已知椭圆
＋
的最小值．
+
=1经过点P（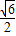
，
），离心率是
，动点M（2，t）（t＞0）