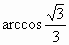Question

如下图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60°,O为球心，则直线OA与截面ABC所成的角是（    ）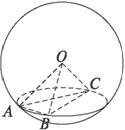

A.arcsin           B.arccos            C.arcsin           D.arccos

Answer 1

解析:设球的半径为R，则4πR²=48π，

∴R²=12.∴R=

在△ABC中，AC²=2²+4²-2×2×4cos60°=12.

∴AC=.设A、B、C三点所在圆的半径为r，则2r=,

∴r=2.

设OA与平面ABC所成的角为θ,则cosθ=.

答案:D