Question

已知函数f(x)=,

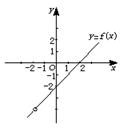
(1)求f(x)的定义域，并作出函数的图像；

(2)求f(x)的不连续点x₀;

(3)对f(x)补充定义，使其是R上的连续函数.

Answer 1

(1) 函数的定义域是(－∞,－2)∪(－2,+∞) (2) 函数f(x)的不连续点是x₀=－2, (3) 将f(x)的表达式改写为f(x)=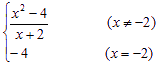

则函数f(x)在R上是连续函数

解析:

 (1)当x+2≠0时，有x≠－2

因此，函数的定义域是(－∞,－2)∪(－2,+∞)

当x≠－2时，f(x)= =x－2,

其图像如上图

(2)由定义域知，函数f(x)的不连续点是x₀=－2.

(3)因为当x≠－2时，f(x)=x－2,

所以=－4 

因此，将f(x)的表达式改写为f(x)=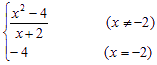

则函数f(x)在R上是连续函数.