题目内容
 (2010•通州区一模)设不等式组
(2010•通州区一模)设不等式组
|
|
(Ⅰ)定义坐标为整数的点为“整点”.在区域U内任取一整点Q,求该点在区域V的概率;
(Ⅱ)在区域U内任取一点M,求该点在区域V的概率.
分析:(I)由题意知本题是一个古典概型,用列举法求出平面区域U的整点的个数,平面区域V的整点个数,即可求出该点在区域V的概率;
(II)因满足:“y≥-x+b”的平面区域是一个弓形区域,欲求y≥-x+b的概率,只须求出弓形区域的面积与圆的面积之比即可.
(II)因满足:“y≥-x+b”的平面区域是一个弓形区域,欲求y≥-x+b的概率,只须求出弓形区域的面积与圆的面积之比即可.
解答: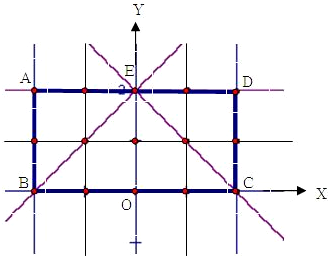 解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,设点Q在区域V的概率为P(Q),则P(Q)=
解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,设点Q在区域V的概率为P(Q),则P(Q)=
=
. (6分)
(Ⅱ)设点M在区域V的概率为P(M),
如图,易知,
区域U的长方形的面积为8,
区域V的三角形的面积为4,
∴P(M)=
=
. (13分)
 解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,设点Q在区域V的概率为P(Q),则P(Q)=
解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,设点Q在区域V的概率为P(Q),则P(Q)=| 9 |
| 15 |
| 3 |
| 5 |
(Ⅱ)设点M在区域V的概率为P(M),
如图,易知,
区域U的长方形的面积为8,
区域V的三角形的面积为4,
∴P(M)=
| 4 |
| 8 |
| 1 |
| 2 |
点评:本题主要考查了古典概型和几何概型,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
| m |
| n |

练习册系列答案
相关题目
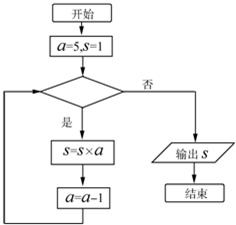 (2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
(2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )