题目内容
已知圆x2+y2=2，直线l与圆O相切于第一象限，切点为C，并且与坐标轴相交于点A、B，则当线段AB最小时，则直线AB方程为（ ）A．x+y=2
B．
C．
D．
【答案】分析：设出直线AB的方程，利用直线l与圆O相切于第一象限，结合基本不等式，即可求得结论．
解答：解：设直线AB的方程为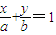
，即bx+ay-ab=0
由题意，直线l与圆O相切于第一象限，∴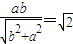
（a＞0，b＞0），∴ab≥4（当且仅当a=b=2时，取等号）
∵AB=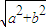
≥
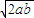≥2
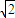
∴a=b=2时，线段AB最小为2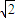
∴直线AB的方程为x+y=2
故选A．
点评：本题考查直线与圆相切问题，考查基本不等式的运用，考查学生的计算能力，属于中档题．
解答：解：设直线AB的方程为
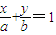，即bx+ay-ab=0由题意，直线l与圆O相切于第一象限，∴
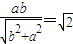（a＞0，b＞0），∴ab≥4（当且仅当a=b=2时，取等号）∵AB=
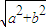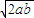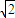
≥≥2∴a=b=2时，线段AB最小为2
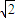
∴直线AB的方程为x+y=2
故选A．
点评：本题考查直线与圆相切问题，考查基本不等式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
出彩同步大试卷系列答案
相关题目