Question

某实验室至少需某种化学药品10kg，现在市场上该药品有两种包装，一种是每袋3kg，价格为12元；另一种是每袋2kg，价格为10元．但由于储存的因素，每一种包装购买的数量都不能超过5袋，则在满足需要的条件下，花费最少为

 

 元．

Answer 1

分析：设价格为12元的x袋，价格为10元y袋，花费为Z百万元，先分析题意，找出相关量之间的不等关系，即x，y满足的约束条件，由约束条件画出可行域；要求应作怎样的组合投资，可使花费最少，即求可行域中的最优解，在线性规划的解答题中建议使用直线平移法求出最优解，即将目标函数看成是一条直线，分析目标函数Z与直线截距的关系，进而求出最优解．

解答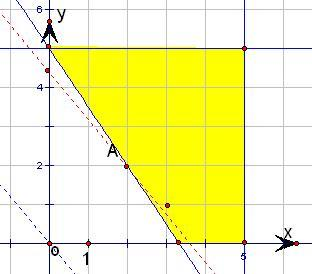：解：设价格为12元的x袋，价格为10元y袋，花费为Z百万元，
则约束条件为：

3x+2y≥10 5≥x≥0 5≤y≥0 x，y∈N

，（5′）目标函数为z=12x+10y，（7′）
作出可行域，（11′）
使目标函数为z=12x+10y取最小值的点（x，y）是
A（2，2）此时z=44（13′）
答：应价格为12元的2袋，价格为10元2袋，花费最少为44元．（15′）
故答案为：44．

点评：在解决线性规划的应用题时，其步骤为：①分析题目中相关量的关系，列出不等式组，即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中．