题目内容
设i、j分别是平面直角坐示系Ox，Oy正方向上的单位向量，且
=-2i+mj，
=ni+j，
=5i-j，若点A、B、C在同一条直线上，且m=2n，求实数m、n的值．
【答案】分析：由A、B、C共线，可找出共线向量，然后由共线向量的性质可解题．
解答：解：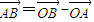
=（n+2）i+（1-m）j，
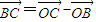=（5-n）i+（-2）j．
∵点A、B、C在同一条直线上，∴
∥
，
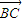即
=λ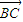
，
∴（n+2）i+（1-m）j=λ[（5-n）i+（-2）j]，
点评：本题主要考查向量的坐标运算和向量的共线问题．在向量中，共线和平行是相同的．
解答：解：
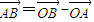=（n+2）i+（1-m）j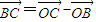，=（5-n）i+（-2）j．∵点A、B、C在同一条直线上，∴
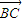∥，即
=λ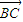，∴（n+2）i+（1-m）j=λ[（5-n）i+（-2）j]，
点评：本题主要考查向量的坐标运算和向量的共线问题．在向量中，共线和平行是相同的．
练习册系列答案
相关题目
=-2i+mj，
=ni+j，
=5i-j，若点A、B、C在同一条直线上，且m=2n，求实数m、n的值．
=-2i+mj，
=ni+j，
=5i-j，若点A、B、C在同一条直线上，且m=2n，求实数m、n的值．