题目内容
已知椭圆 (θ为参数)上的点P到它的两个焦点F1、F2的距离之比
(θ为参数)上的点P到它的两个焦点F1、F2的距离之比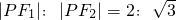 ,且
,且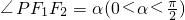 ,则α的最大值为
,则α的最大值为
- A.

- B.

- C.

- D.
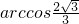
A
分析:本选择题利用特殊值法解决,不妨设|PF1|=2,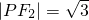 ,|F1F2|=2c,在三角形PF1F2,由余弦定理结合基本不等式得cosα的取值范围,从而得出α的最大值.
,|F1F2|=2c,在三角形PF1F2,由余弦定理结合基本不等式得cosα的取值范围,从而得出α的最大值.
解答:不妨设|PF1|=2,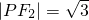 ,|F1F2|=2c,
,|F1F2|=2c,
则2a=2+ ?a=
?a= (2+
(2+ ),
),
∴c<a= (2+
(2+ ),
),
在三角形PF1F2,由余弦定理得:A
cosα=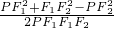 =
=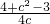 =
=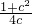 ≥
≥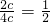
当且仅当c=1时取等号,
cosα的最小值为 ,∵
,∵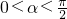 ,
,
则α的最大值为 .
.
故选A.
点评:本小题主要考查椭圆的参数方程、余弦定理、基本不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
分析:本选择题利用特殊值法解决,不妨设|PF1|=2,
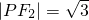 ,|F1F2|=2c,在三角形PF1F2,由余弦定理结合基本不等式得cosα的取值范围,从而得出α的最大值.
,|F1F2|=2c,在三角形PF1F2,由余弦定理结合基本不等式得cosα的取值范围,从而得出α的最大值.解答:不妨设|PF1|=2,
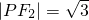 ,|F1F2|=2c,
,|F1F2|=2c,则2a=2+
 ?a=
?a= (2+
(2+ ),
),∴c<a=
 (2+
(2+ ),
),在三角形PF1F2,由余弦定理得:A
cosα=
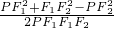 =
=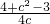 =
=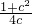 ≥
≥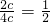
当且仅当c=1时取等号,
cosα的最小值为
 ,∵
,∵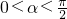 ,
,则α的最大值为
 .
.故选A.
点评:本小题主要考查椭圆的参数方程、余弦定理、基本不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 (t为参数)经过椭圆
(t为参数)经过椭圆 (
( 为参数)的左焦点F.
为参数)的左焦点F. (t为参数)经过椭圆
(t为参数)经过椭圆 (
( 为参数)的左焦点F.
为参数)的左焦点F. (t为参数),与椭圆x2+4y2=16交于A、B两点.
(t为参数),与椭圆x2+4y2=16交于A、B两点. 在M-1的作用下的新曲线的方程.
在M-1的作用下的新曲线的方程. (t为参数),
(t为参数), (θ为参数).
(θ为参数). 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标; 的最大值.
的最大值.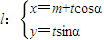 (t为参数)经过椭圆
(t为参数)经过椭圆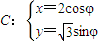 (φ为参数)的左焦点F.
(φ为参数)的左焦点F.