题目内容
10.已知直线l的方程为$\left\{\begin{array}{l}{x=m+t}\\{y=t}\end{array}\right.$(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4$\sqrt{2}$cos(θ+$\frac{π}{4}$)(1)把曲线C的方程化为直角坐标方程,并说明曲线C的形状;
(2)若曲线C上存在点P到直线l的距离为2$\sqrt{2}$,求实数m的取值范围.
分析 (1)利用两角和的余弦展开,两边同时乘以ρ后代入ρ2=x2+y2,x=ρcosθ,y=ρsinθ得答案;
(2)化直线的参数方程为普通方程,画出图形,数形结合求得满足条件的实数m的取值范围.
解答  解:(1)由ρ=4$\sqrt{2}$cos(θ+$\frac{π}{4}$),得$ρ=4\sqrt{2}(cosθcos\frac{π}{4}-sinθsin\frac{π}{4})$=4cosθ-4sinθ,
解:(1)由ρ=4$\sqrt{2}$cos(θ+$\frac{π}{4}$),得$ρ=4\sqrt{2}(cosθcos\frac{π}{4}-sinθsin\frac{π}{4})$=4cosθ-4sinθ,
∴ρ2=4ρ(cosθ-sinθ),即x2+y2-4x+4y=0.
化为标准方程:(x-2)2+(y+2)2=8.
∴曲线C是以(2,-2)为圆心,以$2\sqrt{2}$为半径的圆;
(2)化直线l的方程$\left\{\begin{array}{l}{x=m+t}\\{y=t}\end{array}\right.$为x-y-m=0.
若曲线C上存在点P到直线l的距离为2$\sqrt{2}$,
由图可知,OA=6$\sqrt{2}$,OB=$2\sqrt{2}$,
∴直线x-y-m=0在y轴上截距的范围为[-12,4],
即-m∈[-12,4],
∴m∈[-4,12].
点评 本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
 在三棱椎O-ABC中,OA=OB=OC=1,∠AOB=90°,OC⊥平面AOB,D为AB的中点,则OD与平面OBC的夹角为$\frac{π}{4}$.
在三棱椎O-ABC中,OA=OB=OC=1,∠AOB=90°,OC⊥平面AOB,D为AB的中点,则OD与平面OBC的夹角为$\frac{π}{4}$. 为数列
为数列 的前
的前 项和,已知
项和,已知 ,且
,且 .
. 为等差数列;
为等差数列; ,求数列
,求数列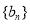 的前
的前 项和.
项和.
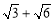 B.
B.
 D.
D.