题目内容
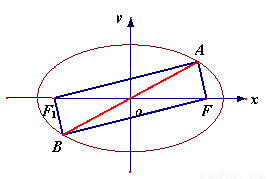
已知椭圆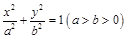 上一点
上一点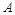 关于原点的对称点为
关于原点的对称点为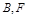 为其右焦点,若
为其右焦点,若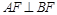 ,设
,设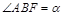 ,且
,且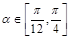 ,则该椭圆离心率的取值范围为( )
,则该椭圆离心率的取值范围为( )
A.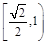 B.
B.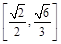 C.
C. D.
D.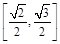
【答案】
B
【解析】
试题分析:∵B和A关于原点对称,∴B也在椭圆上,设左焦点为F′,根据椭圆定义:|AF|+|AF′|=2a,又∵|BF|=|AF′|∴|AF|+|BF|=2a …①,O是Rt△ABF的斜边中点,∴|AB|=2c,又|AF|=2csinα …②,|BF|=2ccosα …③,②③代入①2csinα+2ccosα=2a,∴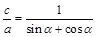 即e=
即e=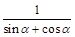 =
=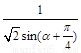 ,∵a∈[
,∵a∈[ ],∴
],∴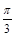 ≤α+π/4≤
≤α+π/4≤ ,∴
,∴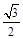 ≤sin(α+
≤sin(α+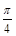 )≤1,∴
)≤1,∴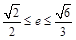 ,故选B
,故选B
考点:本题考查了椭圆离心率的求法
点评:解求离心率问题时要特别利用好椭圆的定义,找出关于a,b,c的不等式,然后得出离心率的范围

练习册系列答案
相关题目
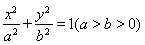
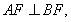
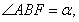
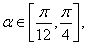
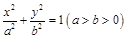 上一点
上一点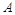 关于原点的对称点为
关于原点的对称点为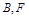 为其右焦点,若
为其右焦点,若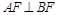 ,设
,设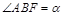 ,且
,且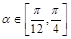 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 . 上一点
上一点 到它的左右两个焦点的距离和是6,
到它的左右两个焦点的距离和是6, 及椭圆离心率的值.
及椭圆离心率的值.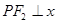 轴(
轴(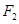 为右焦点),且
为右焦点),且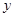 轴上的射影为点
轴上的射影为点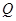 ,求点
,求点