题目内容

5．如果一个正方体的体积在数值上为v，表面积在数值上为s，且v=s+1，那么这个方体的棱长（精确到0.01）约为（　　）
A．5.01B．5.08C．6.03D．6.05

分析 设出正方体的棱长，利用等式关系求解即可．

解答 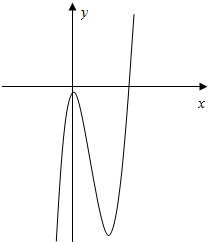解：设正方体的棱长为a，则正方体的体积为：正方体的体积在数值上为v，表面积在数值上为s，且v=s+1，
可得：a3=6a2+1．
画出函数y=x3-6x2-1的图象，函数的零点，
f（6）=63-63-1＜0，
f（6.05）=6.053-6×6.052-1=0.830＞0．
由零点判定定理可知，f（6.03）≈0．
故选：C．

点评 本题考查函数的零点，几何体的体积的应用，函数的图象的应用，考查计算能力．

练习册系列答案
相关题目
15．已知函数f（x）=4-x2
（1）试判断函数f（x）的奇偶性；
（2）用定义证明函数f（x）在[0，+∞）是减函数；
（3）求f（x）在[-1，2]上的最大值和最小值．
16．在正三角形ABC中，D是BC上的点，且AB=4，BD=1，则$\overrightarrow{AB}$•$\overrightarrow{AD}$=（　　）
A．4B．2C．2$\sqrt{3}$D．14
13．直线y=x-$\frac{1}{2}$与抛物线x2=2y的位置关系是相切（填“相交、相切、相离）
20．复数i+i2在复平面内表示的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
10．已知a＞0，若y=3a2+a+$\frac{9}{{a}^{3}}$，则下列说法正确的序号是（　　）
①y有最小值9$\sqrt{3}$；②y有最小值9；③y有最大值9．
A．①B．②C．③D．以上都不正确
17．直线ax+by-2=0（a，b＞0）平分圆x2+y2-4x-2y-8=0的周长，则$\frac{1}{a}$$+\frac{8}{b}$的最小值为9．
14．设函数y=f（x）是定义在R+上的减函数，并且任意的正实数x，y满足f（xy）=f（x）+f（y），f（2$\sqrt{2}$）=1．
（1）求f（1）的值；
（2）求f（8）的值；
（3）如果f（4）+f（x-2）＜2，求x的取值范围．
15．若a1=1，an=-SnSn-1，（n≥2），求an．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网