题目内容
10、已知点M到点F（4，0）的距离比它到直线l：x+5=0的距离小1，点A的坐标为（2，3），则 MA+MF的最小值为
6
．分析：点M到点F（4，0）的距离比它到直线l：x+5=0的距离小1即说明点F（4，0）的距离比它到直线l：x+4=0的距离相等，由此知点M的轨迹是抛物线，写出抛物线的方程，根据抛物线定义得到结果．
解答：解：∵点M到点F（4，0）的距离比它到直线l：x+5=0的距离小1
∴点F（4，0）的距离比它到直线l：x+4=0的距离相等，
根据抛物线的定义知曲线是一条抛物线，
∴点M的轨迹的方程是y=16x2，
∵点A的坐标为（2，3），
∴MA+MF的最小值为过A向x=-4所做的垂线段的长度2-（-4）=6
故答案为：6．
∴点F（4，0）的距离比它到直线l：x+4=0的距离相等，
根据抛物线的定义知曲线是一条抛物线，
∴点M的轨迹的方程是y=16x2，
∵点A的坐标为（2，3），
∴MA+MF的最小值为过A向x=-4所做的垂线段的长度2-（-4）=6
故答案为：6．
点评：本题考查抛物线的定义和抛物线的性质，本题解题的关键是根据所给的到点和到直线之间的距离的关系，得到曲线是一条抛物线，注意抛物线的定义的应用．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
（2013•深圳二模）已知动点 M 到点 F（0，1）的距离与到直线 y=4 的距离之和为 5．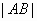
．