题目内容
(08年哈九中)已知在直三棱柱![]() 中,
中,
![]() .
.
(1)证明:![]() ;
;
(2)若![]() 是
是![]() 中点,求点
中点,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的大小 .
的大小 .

解析:(1)证明:连结B1C,
在直线ABC―A1B1C1中,∵BC=CC1
∴四边形ACC1A1是正方形,∴C1B⊥CB。
又∵AC⊥BC,面BC1⊥面ABC
∴AC⊥平面BB1C1C,
∴CB1是斜线AB1在平面CBB1C1的射影
∴AB1⊥BC1
(2)连结A1C与AC1相交于点O
∵AA1CC1为正方形 ∴A1C⊥AC1
又∵平面AA1CC1⊥平面A1B1C1
B1C1⊥A1C1 ∴B1C1⊥平面AA1CC1
∴A1C⊥B1C1
∴A1C⊥平面AB1C1
∴A1O是A1点到平面AB1C1的距离
∵AA1CC1为正方形 AC=CC1=2 ∴A1O=![]()
连结A1M与AB1相交于D ∵M为AB的中点
∴![]() ∴M到平面AB1C1的距离h是A1到平面AB1C1距离的
∴M到平面AB1C1的距离h是A1到平面AB1C1距离的![]()
∴h=![]() 。
。
(3)作OM⊥AB1连结AM ∵A1O⊥平面AB1C1
OM⊥AB1 ∴A1M⊥AB1 ∴∠A1MC是二面角
A1―AB1―C1的平面角。
在矩形AA1BB1中,AC=BC=2 ∠ACB=90° ![]()
又∵AA1=2 ∴AB1=![]()
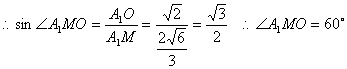
∴二面角C1―AB1―M为大小为120°。

练习册系列答案
相关题目
