题目内容
在△ABC中, 分别为角
分别为角 所对的三边,已知
所对的三边,已知
(Ⅰ)求 的值
的值
(Ⅱ)若 ,求边
,求边 的长.
的长.
(Ⅰ)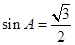 ;(Ⅱ)
;(Ⅱ)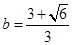 .
.
解析试题分析:(Ⅰ)求 的值,可考虑利用正弦定理,也可利用面积公式
的值,可考虑利用正弦定理,也可利用面积公式 ,但本题已知
,但本题已知 ,显然是余弦定理形式,可考虑利用余弦定理求出
,显然是余弦定理形式,可考虑利用余弦定理求出 ,因此对
,因此对 变形为
变形为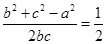 ,可得
,可得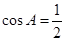 ,从而求出
,从而求出 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求边
,求边 的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知
的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知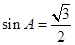 ,只要能求出
,只要能求出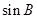 ,利用余弦定理即可解决,由已知
,利用余弦定理即可解决,由已知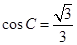 ,利用
,利用 ,根据两角和与差的正弦公式即可求出,从而求出边
,根据两角和与差的正弦公式即可求出,从而求出边 的长.
的长.
试题解析:(Ⅰ)∵b2+c2-a2=bc,cosA=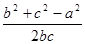 =
=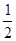 (3分)
(3分)
又∵ ∴sinA=
∴sinA=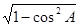 =
=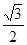 (5分)
(5分)
(Ⅱ)在△ABC中,sinA=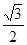 ,a=
,a=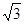 ,cosC=
,cosC=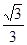
可得sinC=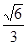 (6分)
(6分)
∵A+B+C=p
∴sinB ="sin(A+C)=" 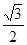 ×
×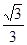 +
+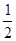 ×
×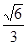 =
= (9分)
(9分)
由正弦定理知: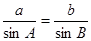
∴b= =
= =
=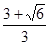 . (12分)
. (12分)
考点:解三角形.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知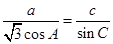 ,
, 的大小;(2)若
的大小;(2)若 求
求 的值.
的值. 为
为 ,
, 的等差中项.
的等差中项. 中,已知
中,已知 ,
, 是
是 边上的一点,
边上的一点,

 的值;
的值; 的值。
的值。 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,已知
,已知 ,
, .
. ,求
,求 ,求
,求 中,已知点
中,已知点 在
在 边上,满足
边上,满足 ,
, ,
, ,
, .
.
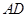 的长;
的长; .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的大小;
的大小; ,求
,求 的顶点
的顶点 ,顶点
,顶点 在直线
在直线 上;
上; 求点
求点 ,且
,且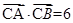 ,求角
,求角