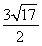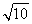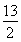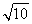题目内容
已知四棱锥P－ABCD的正视图是一个底边长为4、腰长为3的等腰三角形，如图分别是四棱锥P－ABCD的侧视图和俯视图．
(1)求证：AD⊥PC；
(2)求四棱锥P－ABCD的侧面PAB的面积．
（1）见解析（2）6
【解析】(1)证明：依题意，可知点P在平面ABCD上的射影是线段CD的中点E，如图，连接PE，则PE⊥平面ABCD.
∵AD?平面ABCD，∴AD⊥PE.
∵AD⊥CD，CD∩PE＝E，CD?平面PCD，PE?平面PCD，∴AD⊥平面PCD.
∵PC?平面PCD，∴AD⊥PC.
(2)依题意，在等腰三角形PCD中，PC＝PD＝3，DE＝EC＝2，在Rt△PED中，PE＝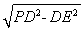 
＝
.
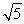过点E作EF⊥AB，垂足为F，连接PF，
∵PE⊥平面ABCD，AB?平面ABCD，∴AB⊥PE.
∵EF?平面PEF，PE?平面PEF，EF∩PE＝E，∴AB⊥平面PEF.
∵PF?平面PEF，∴AB⊥PF.
依题意得EF＝AD＝2.
在Rt△PEF中，PF＝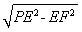 
＝3，
∴△PAB的面积S＝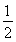
·AB·PF＝6.
∴四棱锥P－ABCD的侧面PAB的面积为6
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
