题目内容
(09年海淀区二模理)(13分)
已知抛物线C:![]() ,过定点
,过定点![]()
![]() ,作直线
,作直线![]() 交抛物线于
交抛物线于![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)当点A是抛物线C的焦点,且弦长![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .求证:点B的坐标是
.求证:点B的坐标是![]() 并求点
并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
解析:(Ⅰ)由抛物线C:![]() 得抛物线的焦点坐标为
得抛物线的焦点坐标为![]() ,设直线
,设直线![]() 的方程为:
的方程为:![]() ,
,![]() . ………………………………1分
. ………………………………1分
由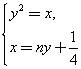 得
得![]() .
.
所以![]() ,
,![]() .因为
.因为![]() , …………………3分
, …………………3分
所以![]() .
.
所以![]() .即
.即![]() .
.
所以直线![]() 的方程为:
的方程为:![]() 或
或![]() . ………………………5分
. ………………………5分
(Ⅱ)设![]() ,
,![]() ,则
,则![]() .
.
由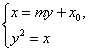 得
得![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() . ……………………………………7分
. ……………………………………7分
()设![]() ,则
,则![]() .
.
由题意知:![]() ∥
∥![]() ,
,![]() .
.
即![]() .
.
显然![]() …………………9分
…………………9分
()由题意知:![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,即
,即![]() ,即
,即![]() .
.
![]() .
. ![]() .
.
![]() .
.![]()
![]() ,
,![]() . ………………………………11分
. ………………………………11分
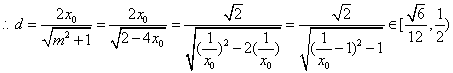 .
.
即![]() 的取值范围是
的取值范围是![]() . ………………………………………13分
. ………………………………………13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目