题目内容
设z1=1-cosθ+isinθ,z2=a2+ai(a∈R),若z1z2≠0,z1z2-. | z1z2 |
分析:这是一道探索性问题.可根据复数的概念与纯虚数的性质及复数为实数的充要条件,直接进行解答.
解答:解:假设满足条件的θ存在.
因z1z2≠0,z1z2-
=0,故z1z2为纯虚数.
又z1z2=(1-cosθ+isinθ)(a2+ai)
=[a2(1-cosθ)-asinθ]+[a(1-cosθ)+a2sinθ]i,
于是,
由②知a≠0.
因θ∈(0,2π),故cosθ≠1.于是,由①得a=
.
另一方面,因(z1-z2)2∈R,故z1-z2为实数或为纯虚数.
又z1-z2=1-cosθ-a2+(sinθ-a)i,
于是sinθ-a=0,或1-cosθ-a2=0.
若sinθ-a=0,则由方程组
得
=sinθ,故cosθ=0,于是θ=
或θ=
.
若1-cosθ-a2=0,则由方程组
得(
)2=1-cosθ.
由于sin2θ=1-cos2θ=(1+cosθ)(1-cosθ),故1+cosθ=(1-cosθ)2.
解得cosθ=0,从而θ=
或θ=
.
综上所知,在(0,2π)内,存在θ=
或θ=
,使(z1-z2)2为实数.
因z1z2≠0,z1z2-
. |
| z1z2 |
又z1z2=(1-cosθ+isinθ)(a2+ai)
=[a2(1-cosθ)-asinθ]+[a(1-cosθ)+a2sinθ]i,
于是,
|
由②知a≠0.
因θ∈(0,2π),故cosθ≠1.于是,由①得a=
| sinθ |
| 1-cosθ |
另一方面,因(z1-z2)2∈R,故z1-z2为实数或为纯虚数.
又z1-z2=1-cosθ-a2+(sinθ-a)i,
于是sinθ-a=0,或1-cosθ-a2=0.
若sinθ-a=0,则由方程组
|
得
| sinθ |
| 1-cosθ |
| π |
| 2 |
| 3π |
| 2 |
若1-cosθ-a2=0,则由方程组
|
| sinθ |
| 1-cosθ |
由于sin2θ=1-cos2θ=(1+cosθ)(1-cosθ),故1+cosθ=(1-cosθ)2.
解得cosθ=0,从而θ=
| π |
| 2 |
| 3π |
| 2 |
综上所知,在(0,2π)内,存在θ=
| π |
| 2 |
| 3π |
| 2 |
点评:①解题技巧:解题中充分使用了复数的性质:z≠0,z+z=0?z∈{纯虚数}?
以及z2∈R?z∈R或z∈{纯虚数}.(注:Re(z),Im(z)分别表示复数z的实部与虚部)
②解题规律:对于“是否型存在题型”,一般处理方法是首先假设结论成立,再进行正确的推理,
若无矛盾,则结论成立;否则结论不成立.
|
以及z2∈R?z∈R或z∈{纯虚数}.(注:Re(z),Im(z)分别表示复数z的实部与虚部)
②解题规律:对于“是否型存在题型”,一般处理方法是首先假设结论成立,再进行正确的推理,
若无矛盾,则结论成立;否则结论不成立.

练习册系列答案
相关题目
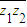 =0,问在(0,2π)内是否存在θ使(z1-z2)2为实数?若存在,求出θ的值;若不存在,请说明理由.
=0,问在(0,2π)内是否存在θ使(z1-z2)2为实数?若存在,求出θ的值;若不存在,请说明理由.