题目内容
(本题14分)阅读：设Z点的坐标(a, b)，r=|
|，θ是以x轴的非负半轴为始边、以OZ所在的射线为终边的角，复数z=a+bi还可以表示为z=r(cosθ+isinθ)，这个表达式叫做复数z的三角形式，其中，r叫做复数z的模，当r≠0时，θ叫做复数z的幅角，复数0的幅角是任意的，当0≤θ<2π时，θ叫做复数z的幅角主值，记作argz．
根据上面所给出的概念，请解决以下问题：
(1)设z=a+bi =r(cosθ+isinθ) (a、bÎR，r≥0)，请写出复数的三角形式与代数形式相互之间的转换关系式；
(2)设z1=r1(cosθ1+isinθ1)，z2=r2(cosθ2+isinθ2)，探索三角形式下的复数乘法、除法的运算法则，请写出三角形式下的复数乘法、除法的运算法则．(结论不需要证明)
解：(1)
；
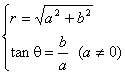……(各3分)………………………6分
(以上每组内只写出一个，给2分)
(2) 三角形式下的复数乘法的运算法则：
z1z2=r1(cosθ1+isinθ1)´ r2(cosθ2+isinθ2)=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]……10分
三角形式下的复数除法的运算法则：
[cos(θ1–θ2)+isin(θ1–θ2)] (z2≠0)…………14分
注意：z2≠0不写扣1分．
练习册系列答案
相关题目