ƒøƒ⁄»ð
°æƒø°ø“—÷™∫Ø ˝f£®x£©= ![]() £¨∆‰÷–[x]±Ì æ≤ª≥¨π˝xµƒ◊Ó¥Û’˚ ˝£Æ…Ën° N* £¨ ∂®“Â∫Ø ˝fn£®x£©£∫f1£®x£©=f£®x£©£¨f2£®x£©=f£®f1£®x£©£©£¨°≠£¨fn£®x£©=f£®fn©Å1£®x£©£©£®n°ð2£©£¨‘Úœ¬¡–Àµ∑®’˝»∑µƒ”– ¢Ÿy=
£¨∆‰÷–[x]±Ì æ≤ª≥¨π˝xµƒ◊Ó¥Û’˚ ˝£Æ…Ën° N* £¨ ∂®“Â∫Ø ˝fn£®x£©£∫f1£®x£©=f£®x£©£¨f2£®x£©=f£®f1£®x£©£©£¨°≠£¨fn£®x£©=f£®fn©Å1£®x£©£©£®n°ð2£©£¨‘Úœ¬¡–Àµ∑®’˝»∑µƒ”– ¢Ÿy= ![]() µƒ∂®“”ڌ™
µƒ∂®“”ڌ™ ![]() £ª
£ª
¢⁄…ËA={0£¨1£¨2}£¨B={x|f3£®x£©=x£¨x° A}£¨‘ÚA=B£ª
¢€ ![]() £ª
£ª
¢Ð»ÙºØ∫œM={x|f12£®x£©=x£¨x° [0£¨2]}£¨
‘ÚM÷–÷¡…Ÿ∫¨”–8∏ˆ‘™Àÿ£Æ£® £©
A.1∏ˆ
B.2∏ˆ
C.3∏ˆ
D.4∏ˆ
°æ¥∞∏°øC
°æΩ‚Œˆ°øΩ‚£∫µ±0°Ðx£º1 ±£¨f£®x£©=2£®1©Åx£©£ª µ±1°Ðx°Ð2 ±£¨f£®x£©=x©Å1£Æ
º¥”–f£®x£©= ![]() £¨
£¨
ª≠≥ˆy=f£®x£©‘⁄[0£¨2]µƒÕºœÛ£Æ
∂‘”⁄¢Ÿ£¨ø…µ√f£®x£©°Ðx£¨µ±1°Ðx°Ð2 ±£¨x©Å1°Ðx≥…¡¢£ª
µ±0°Ðx£º1 ±£¨2£®1©Åx£©°Ðx£¨Ω‚µ√ ![]() °Ðx£º1£¨º¥”–∂®“”ڌ™{x|
°Ðx£º1£¨º¥”–∂®“”ڌ™{x| ![]() °Ðx°Ð2}£¨
°Ðx°Ð2}£¨
π ¢Ÿ’˝»∑£ª
∂‘”⁄¢⁄£¨µ±x=0 ±£¨f3£®0£©=f[f2£®0£©]=f£®f£®f£®0£©£©£©=f£®f£®2£©£©=f£®1£©=0≥…¡¢£ª
µ±x=1 ±£¨f3£®1£©=f[f2£®1£©]=f£®f£®f£®1£©£©£©=f£®f£®0£©£©=f£®2£©=1≥…¡¢£ª
µ±x=2 ±£¨f3£®2£©=f[f2£®2£©]=f£®f£®f£®2£©£©£©=f£®f£®1£©£©=f£®0£©=2≥…¡¢£ª
º¥”–A=B£¨π ¢⁄’˝»∑£ª
∂‘”⁄¢€£¨f1£® ![]() £©=2£®1©Å
£©=2£®1©Å ![]() £©=
£©= ![]() £¨f2£®
£¨f2£® ![]() £©=f£®f£®
£©=f£®f£® ![]() £©£©=f£®
£©£©=f£® ![]() £©=2£®1©Å
£©=2£®1©Å ![]() £©=
£©= ![]() £¨
£¨
f3£® ![]() £©=f£®f2£®
£©=f£®f2£® ![]() £©£©=f£®
£©£©=f£® ![]() £©=
£©= ![]() ©Å1=
©Å1= ![]() £¨f4£®
£¨f4£® ![]() £©=f£®f3£®
£©=f£®f3£® ![]() £©£©=f£®
£©£©=f£® ![]() £©=2£®1©Å
£©=2£®1©Å ![]() £©=
£©= ![]() £¨
£¨
“ª∞„µÿ£¨f4k+r£® ![]() £©=fr£®
£©=fr£® ![]() £©£®k£¨r° N£©£Æ
£©£®k£¨r° N£©£Æ
º¥”–f2016£® ![]() £©+f2017£®
£©+f2017£® ![]() £©=f4£®
£©=f4£® ![]() £©+f1£®
£©+f1£® ![]() £©=
£©= ![]() +
+ ![]() =
= ![]() £¨π ¢€≤ª’˝»∑£ª
£¨π ¢€≤ª’˝»∑£ª
∂‘”⁄¢Ð£¨”…£®1£©÷™£¨f£® ![]() £©=
£©= ![]() £¨°ýfn£®
£¨°ýfn£® ![]() £©=
£©= ![]() £¨‘Úf12£®
£¨‘Úf12£® ![]() £©=
£©= ![]() £¨°ý
£¨°ý ![]() ° M£Æ
° M£Æ
”…£®2£©÷™£¨∂‘x=0°¢1°¢2£¨∫„”–f3£®x£©=x£¨°ýf12£®x£©=x£¨‘Ú0°¢1°¢2° M£Æ
”…£®3£©÷™£¨∂‘x= ![]() °¢
°¢ ![]() °¢
°¢ ![]() °¢
°¢ ![]() £¨∫„”–f12£®x£©=x£¨°ý
£¨∫„”–f12£®x£©=x£¨°ý ![]() °¢
°¢ ![]() °¢
°¢ ![]() °¢
°¢ ![]() ° M£Æ
° M£Æ
◊€…œÀ˘ ˆ ![]() °¢0°¢1°¢2°¢
°¢0°¢1°¢2°¢ ![]() °¢
°¢ ![]() °¢
°¢ ![]() °¢
°¢ ![]() ° M£Æ
° M£Æ
°ýM÷–÷¡…Ÿ∫¨”–8∏ˆ‘™Àÿ£Æπ ¢Ð’˝»∑£Æ
π —°£∫C£Æ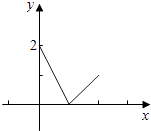

°æƒø°ø![]() ƒÍ
ƒÍ![]() ‘¬
‘¬![]() »’£¨°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±‘⁄…Ω∂´«ýµ∫ø™ƒª.Œ™¡ÀΩ‚ƒƒ–©»À∏¸πÿ◊¢°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±£¨ƒ≥ª˙ππÀʪ˙≥È»°¡ÀƒÍ¡‰‘⁄
»’£¨°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±‘⁄…Ω∂´«ýµ∫ø™ƒª.Œ™¡ÀΩ‚ƒƒ–©»À∏¸πÿ◊¢°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±£¨ƒ≥ª˙ππÀʪ˙≥È»°¡ÀƒÍ¡‰‘⁄![]() -
-![]() ÀÍ÷ƺ‰µƒ
ÀÍ÷ƺ‰µƒ![]() »ÀΩ¯––µ˜≤È£¨≤¢∞¥ƒÍ¡‰ªÊ÷∆≥…∆µ¬ ∑÷≤º÷±∑ΩÕº£¨»ÁÕºÀ˘ 棨∆‰∑÷◊È«¯º‰Œ™£∫
»ÀΩ¯––µ˜≤È£¨≤¢∞¥ƒÍ¡‰ªÊ÷∆≥…∆µ¬ ∑÷≤º÷±∑ΩÕº£¨»ÁÕºÀ˘ 棨∆‰∑÷◊È«¯º‰Œ™£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .∞—ƒÍ¡‰¬‰‘⁄«¯º‰
.∞—ƒÍ¡‰¬‰‘⁄«¯º‰![]() ∫Õ
∫Õ![]() ƒ⁄µƒ»À∑÷±≥∆Œ™°∞«ý…ŸƒÍ°±∫Õ°∞÷–¿œƒÍ°±.
ƒ⁄µƒ»À∑÷±≥∆Œ™°∞«ý…ŸƒÍ°±∫Õ°∞÷–¿œƒÍ°±.

πÿ◊¢ | ≤ªπÿ◊¢ | ∫œº∆ | |
«ý…ŸƒÍ |
| ||
÷–¿œƒÍ | |||
∫œº∆ |
|
|
|
£®1£©∏˘æð∆µ¬ ∑÷≤º÷±∑ΩÕº«Û—˘±æµƒ÷–Œª ˝£®±£¡Ù¡ΩŒª–° ˝£©∫Õ÷⁄ ˝£ª
£®2£©∏˘æð“—÷™Ãıº˛ÕÍ≥…![]() ¡–¡™±Ì£¨≤¢≈–∂œƒÐ∑Ò”–
¡–¡™±Ì£¨≤¢≈–∂œƒÐ∑Ò”–![]() µƒ∞—Œ’»œŒ™°∞÷–¿œƒÍ°±±»°∞«ý…ŸƒÍ°±∏¸º”πÿ◊¢°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±£ª
µƒ∞—Œ’»œŒ™°∞÷–¿œƒÍ°±±»°∞«ý…ŸƒÍ°±∏¸º”πÿ◊¢°∞π˙º ΩÔ˝–≈œ¢ªØ¥Ûª·°±£ª
