题目内容
直线l是双曲线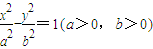
的右准线，以原点为圆心且过双曲线的顶点的圆，被直线l分成弧长为2：1的两段圆弧，则该双曲线的离心率是 ．
【答案】分析：根据圆被分成的两段圆弧的弧长比为2：1，可以求出两个交点与圆心构成的圆心角为120度，根据对称性，在第一象限的交点A原点O所构成直线的倾斜角为60度，记右准线与x轴的交点为B． 则可根据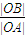
cos60°求得a和c的关系，进而求得离心率e．
解答：解：c2=a2+b2
由于圆被分成的两段圆弧的弧长比为2：1，
所以可以求出两个交点与圆心构成的圆心角为120°，
根据对称性，在第一象限的交点A原点O所构成直线的倾斜角为60°
记右准线与x轴的交点为B．
所以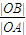
=
=
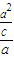=cos60°=
所以e=
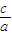=2．
故答案为2．
点评：本题主要考查了双曲线的简单性质．考查了学生对基础知识的熟练程度．
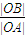cos60°求得a和c的关系，进而求得离心率e．解答：解：c2=a2+b2
由于圆被分成的两段圆弧的弧长比为2：1，
所以可以求出两个交点与圆心构成的圆心角为120°，
根据对称性，在第一象限的交点A原点O所构成直线的倾斜角为60°
记右准线与x轴的交点为B．
所以
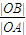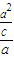===cos60°=所以e=
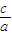=2．故答案为2．
点评：本题主要考查了双曲线的简单性质．考查了学生对基础知识的熟练程度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的右准线，以原点为圆心且过双曲线的顶点的圆，被直线l分成弧长为2 : 1的两段圆弧，则该双曲线的离心率是
C．
D．
的右准线，如果在直线l上存在一点M，使得线段OM(O为坐标原点)的垂直平分线过右焦点，则椭圆的离心率的取值范围是
：
的右准线与一条渐近线交于点
，
是右焦点，若
，且双曲线
。
（0，1）的直线l与双曲线
、
，且
且
，求直线l斜率
的取值范围。
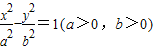的右准线，以原点为圆心且过双曲线的顶点的圆，被直线l分成弧长为2：1的两段圆弧，则该双曲线的离心率是 ．