题目内容
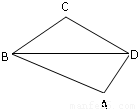
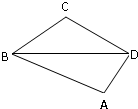 已知一小石子等可能地落入如图所示的四边形ABCD内,如果通过大量的试验发现石子落入△CBD内的频率在
已知一小石子等可能地落入如图所示的四边形ABCD内,如果通过大量的试验发现石子落入△CBD内的频率在| 3 |
| 7 |
分析:设石子落入△BCD内的频率为P1,石子落入△BAD内的频率为P2,且点C和点A到时直线BD的距离d1,d2.根据几何概型,其面积之比即为概率之比,而△BCD与△BAD有公共的底边,由此建立关系式即可求出点A和点C到直线BD的距离之比.
解答:解:设点C和A点到直线BD的距离分别为d1,d2,
石子落入△BCD内的频率为P1,石子落入△BAD内的频率为P2
根据题意得:P1=
,且P2=1-P1=1-
=
又∵P1=
=
,P2=
=
∴
=
=
=
,即点A和点C到直线BD的距离之比为
故选:C
石子落入△BCD内的频率为P1,石子落入△BAD内的频率为P2
根据题意得:P1=
| 3 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
又∵P1=
| S△BCD |
| SABCD |
| ||
| SABCD |
| S△BAD |
| SABCD |
| ||
| SABCD |
∴
| P2 |
| P1 |
| d2 |
| d1 |
| ||
|
| 4 |
| 3 |
| 4 |
| 3 |
故选:C
点评:本题给出共底的两个三角形△BCD与△BAD,在已知石子落入△CBD内的频率的情况下,求点A和点C到直线BD的距离之比.着重考查了几何概型和三角形面积公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
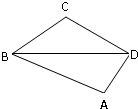 已知一小石子等可能地落入如图所示的四边形ABCD内,如果通过大量的试验发现石子落入△CBD内的频率在
已知一小石子等可能地落入如图所示的四边形ABCD内,如果通过大量的试验发现石子落入△CBD内的频率在 附近,那么点A和点C到直线BD的距离之比为
附近,那么点A和点C到直线BD的距离之比为


 附近,那么点A和点C到直线BD的距离之比为( )
附近,那么点A和点C到直线BD的距离之比为( )