题目内容
定义在R上的函数y=f（x），满足f（3-x）=f（x），（x-
）f′（x）＜0，若x1＜x2，且x1+x2＞3则f（x1）、f（x2）的大小关系为________．
f（x1）＞f（x2）
分析：由“f（3-x）=f（x）”，知函数图象关于直线x=对称，再由“
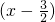f′（x）＜0”可知：当x＞时，函数是减函数，当x＜时，函数是增函数，最后由“x1＜x2，且x1+x2＞3”，得知3-x2＜x1＜x2且x2∈（ ，+∞），结合图象得到结论．
解答：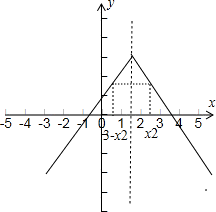
解：∵f（3-x）=f（x），∴函数图象关于直线x=对称，
又∵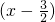f′（x）＜0∴当x＞时，函数是减函数
当x＜时，函数是增函数
∵x1＜x2，且x1+x2＞3
∴3-x2＜x1＜x2且x2∈（，+∞），
观察图象得：f（x1）＞f（x2）
故答案为：f（x1）＞f（x2）．
点评：本题主要考查函数的对称性和单调性、导数、函数单调性的应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题
分析：由“f（3-x）=f（x）”，知函数图象关于直线x=
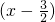对称，再由“f′（x）＜0”可知：当x＞时，函数是减函数，当x＜时，函数是增函数，最后由“x1＜x2，且x1+x2＞3”，得知3-x2＜x1＜x2且x2∈（ ，+∞），结合图象得到结论．解答：
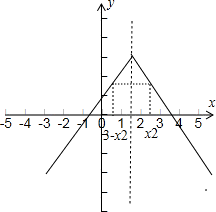解：∵f（3-x）=f（x），∴函数图象关于直线x=对称，又∵
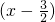f′（x）＜0∴当x＞时，函数是减函数当x＜
时，函数是增函数∵x1＜x2，且x1+x2＞3
∴3-x2＜x1＜x2且x2∈（
，+∞），观察图象得：f（x1）＞f（x2）
故答案为：f（x1）＞f（x2）．
点评：本题主要考查函数的对称性和单调性、导数、函数单调性的应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题
练习册系列答案
阅读快车系列答案
相关题目