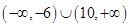题目内容
设
分别为
和椭圆
上的点，则两点间的最大距离是（ ）
B.
C.
D.
D
解析试题分析：依题意两点间的最大距离可以转化为圆心到椭圆上的点的最大距离再加上;圆的半径
.设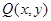
.圆心到椭圆的最大距离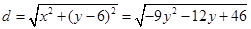
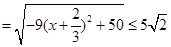.所以两点间的最大距离是.故选D.
考点：1.直线与圆的位置关系.2.数形结合的思想.
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
抛物线
的准线方程是
，则
的值为（ ）
A． | B． | C．8 | D． |
已知
为双曲线
:
的一个焦点，则点到的一条渐近线的距离为（ ）
A． | B．3 | C． | D． |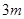
已知双曲线
的一条渐近线平行于直线
：
，双曲线的一个焦点在直线上，则双曲线的方程为
A． | B． |
C． | D． |
的左右焦点为
，直线
过点
且垂直于椭圆的长轴，动直线
垂直于直线
的垂直平分线与
，若
是
，则
的取值范围是（ ）
（5分）（2011•陕西）设抛物线的顶点在原点，准线方程为x=﹣2，则抛物线的方程是（ ）
| A．y2=﹣8x | B．y2=8x | C．y2=﹣4x | D．y2=4x |
已知双曲线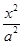
－
＝1(a＞0，b＞0)的两条渐近线均和圆C：x2＋y2－6x＋5＝0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为( )
A． － ＝1 | B． － ＝1 |
C． － ＝1 | D． － ＝1 |
