题目内容
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示)，在窗框为定长的条件下，要使窗户能够透过最多的光线，窗户应设计成怎样的尺寸？
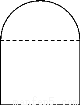
半圆直径与矩形的高的比为2∶1
【解析】设半圆直径为2R,矩形的高为a，
则2a＋2R＋πR＝L(定值)，
S＝2Ra＋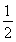
πR2＝－
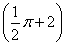R2＋LR，
当R＝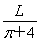
时S最大，此时
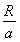＝1，
即半圆直径与矩形的高的比为2∶1时，窗户能够透过最多的光线．
练习册系列答案
相关题目
题目内容
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示)，在窗框为定长的条件下，要使窗户能够透过最多的光线，窗户应设计成怎样的尺寸？
半圆直径与矩形的高的比为2∶1
【解析】设半圆直径为2R,矩形的高为a，
则2a＋2R＋πR＝L(定值)，
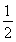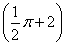S＝2Ra＋πR2＝－R2＋LR，
当R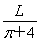＝时S最大，此时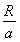＝1，
即半圆直径与矩形的高的比为2∶1时，窗户能够透过最多的光线．
