题目内容
函数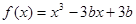 在
在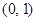 内有极小值,则
内有极小值,则
A.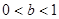 | B.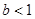 | C.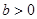 | D. |
A
解析试题分析:因为函数在(0,1)内有极小值,所以极值点在(0,1)上.
令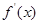 =3
=3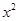 -3b=0,得
-3b=0,得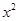 =b,显然b>0,
=b,显然b>0,
∴x=±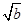 .又∵x∈(0,1),∴0<
.又∵x∈(0,1),∴0<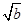 <1.∴0<b<1.故选A.
<1.∴0<b<1.故选A.
考点:利用导数研究函数的极值与参数的范围问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对任意的x∈R,函数f(x)=x3+ax2+7ax不存在
极值点的充要条件是( )
| A.a=0或a="7" | B.a<0或a>21 | C.0≤a≤21 | D.a=0或a=21 |
下列求导数运算正确的是( )
A.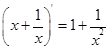 | B.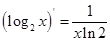 |
C.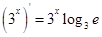 | D.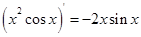 |
已知函数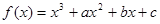 有两个极值点
有两个极值点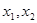 ,若
,若 ,则关于
,则关于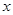 的方程
的方程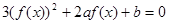 的不同实根个数为 ( )
的不同实根个数为 ( )
| A.3 | B.4 | C.5 | D.6 |
设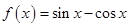 ,则
,则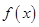 在
在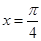 处的导数
处的导数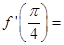 ( )
( )
A.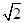 | B.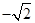 | C.0 | D. |
若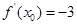 ,则
,则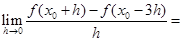 ( )
( )
A.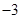 | B.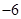 | C.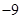 | D.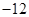 |
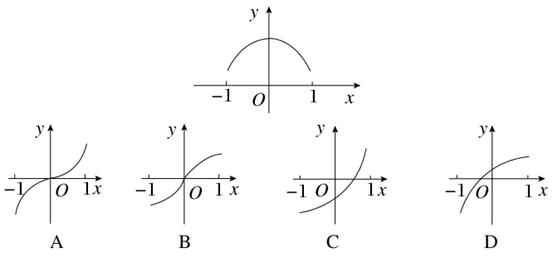
若f(x)=2lnx﹣x2,则f′(x)>0的解集为( )
| A.(0,1) |
| B.(﹣∞,﹣1)∪(0,1) |
| C.(﹣1,0)∪(1,+∞) |
| D.(1,+∞) |
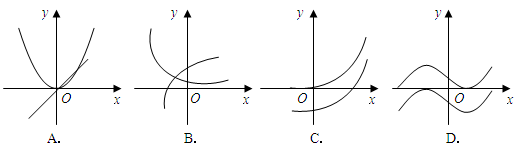
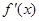 是函数
是函数 的导函数,将
的导函数,将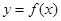 和
和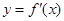 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )