题目内容
【题目】设整数![]() 模2014互不同余,整数
模2014互不同余,整数![]() 模2014也互不同余.证明:可将
模2014也互不同余.证明:可将![]() 重新排列为
重新排列为![]() ,使得
,使得![]() 模4028互不同余.
模4028互不同余.
【答案】见解析
【解析】
记![]() .不妨设
.不妨设
![]() .
.
对每个整数![]() ,若
,若
![]() ,
,
则令![]() ;
;
否则,令![]() .
.
若为前一种情形, 则
![]() .
.
若为后一种情形,则
![]() .
.
若不然,有
![]() ,
,
![]() .
.
上面两式相加得
![]() .
.
于是,![]() .
.
但![]() 模2014(=2k)互不同余,特别地,
模2014(=2k)互不同余,特别地,![]() ,矛盾.
,矛盾.
由上述构造方法知![]() 模4k互不同余.即只需证明结论:对任意整数
模4k互不同余.即只需证明结论:对任意整数![]() ,
,![]() 模4k两两不同余.
模4k两两不同余.
注意到,前面的构造方式已保证
![]() . ①
. ①
[情形1]![]() ,且
,且![]() .
.
则由前面的构造方式知
![]() ,
,
![]() .
.
由于![]() ,故易知
,故易知![]() 与
与![]() 及
及![]() 模2k不同余,
模2k不同余,![]() 与
与![]() 及
及![]() 模2k不同余,从而,模4k更不同余,再结合式①,结论得证.
模2k不同余,从而,模4k更不同余,再结合式①,结论得证.
[情形2]![]() ,且
,且![]() .
.
则由前面的构造方式知
![]() ,
,
![]() .
.
同样有![]() 与
与![]() 及
及![]() 模2k不同余,
模2k不同余,![]() 与
与![]() 及
及![]() 模2k不同余.
模2k不同余.
与情形1相同知结论得证.
[情形3] ![]() ,且
,且![]() (
(![]() ,且
,且![]() 的情形与此相同).
的情形与此相同).
则由前面的构造方式知
![]() ,
,
![]() .
.
由于k为奇数,则![]() .
.
故![]() .
.
因此,![]() 与
与![]() 及
及![]() 模2k不同余,
模2k不同余,![]() 与
与![]() 及
及![]() 模2k不同余.从而,结论得证.
模2k不同余.从而,结论得证.
综上,本题得证.

练习册系列答案
相关题目
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
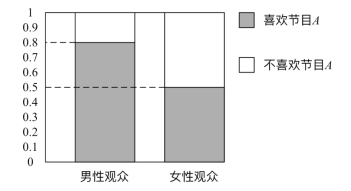
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: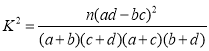
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |




