Question

正三棱锥的底面边长为a，高为

6

6

a，则此棱锥的侧面积等于（　　）

• A、

  3

  4

  a²
• B、

  3

  2

  a²
• C、

  3 3

  4

  a²
• D、

  3 3

  2

  a²

Answer 1

分析：本题考查的是正三棱锥的侧面积求解问题．在解答时，应先求解正三棱锥的底面三角形的高然后利用直角三角形计算出正三棱锥的侧棱长，结合侧面等腰三角形中腰长即侧棱长、底为a，即可求解侧面三角形的面积，进而问题获得解答．

解答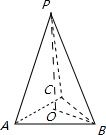：解：由题意可知：如图
在正三角形ABC中：OB=

2

3

•a•

3

2

=

3

3

a，
所以在直角三角形POB中：PB=

PO2+BO2

=

a2 6 + a2 3

=

2

2

a，
∴侧面等腰三角形底边上的高为：

a2 2 - a2 4

=

a

2

，
∴三棱柱的侧面积为：S_侧=3×

1

2

×a×

a

2

=

3

4

a2．
故选A．

点评：本题考查的是正三棱锥的侧面积求解问题．在解答的过程当中充分体现了问题转化的思想、勾股定理的知识以及面积公式的应用．值得同学们体会反思．