题目内容
设命题P:对任意实数,不等式x2-2x>m恒成立;命题:方程
+
=1表示焦点在x轴上的双曲线.
(Ⅰ)若命题q为真命题,求实数m的取值范围;
(Ⅱ)若命题“p∨q””为真命题,且“p∧q”为假命题,求实数m的取值范围.
| x2 |
| m-3 |
| y2 |
| 5-m |
(Ⅰ)若命题q为真命题,求实数m的取值范围;
(Ⅱ)若命题“p∨q””为真命题,且“p∧q”为假命题,求实数m的取值范围.
(1)若方程
+
=1表示焦点在x轴上的双曲线,
则
?m>5
即命题q为真命题时,实数m的取值范围是(5,+∞)(5分)
(2)若命题p真,即对任意实数,不等式x2-2x-m>0恒成立.
∴△=4+4m<0,可得m<-1
p∨q为真命题,p∧q为假命题,说明“p真q假”成立,或“p假q真”成立,
①如果“p真q假”成立,则有
?m<-1(9分)
②如果“p假q真”成立,则有
?m>5(12分)
所以实数的取值范围为m<-1或m>5(13分)
| x2 |
| m-3 |
| y2 |
| 5-m |
则
|
即命题q为真命题时,实数m的取值范围是(5,+∞)(5分)
(2)若命题p真,即对任意实数,不等式x2-2x-m>0恒成立.
∴△=4+4m<0,可得m<-1
p∨q为真命题,p∧q为假命题,说明“p真q假”成立,或“p假q真”成立,
①如果“p真q假”成立,则有
|
②如果“p假q真”成立,则有
|
所以实数的取值范围为m<-1或m>5(13分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
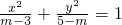 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.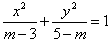 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,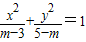 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.