题目内容
设命题p:对任意实数x,不等式x2-2x>m恒成立;命题q:方程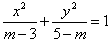 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,
(Ⅰ)若命题q为真命题,求实数m的取值范围;
(Ⅱ)若命题“p∨q”为真命题,且“p∧q”为假命题,求实数m的取值范围。
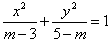 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,(Ⅰ)若命题q为真命题,求实数m的取值范围;
(Ⅱ)若命题“p∨q”为真命题,且“p∧q”为假命题,求实数m的取值范围。
解:(1)方程 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,
 ,
,
即命题q为真命题时,实数m的取值范围是m>5;
(2)若命题p真,即对任意实数x,不等式 恒成立,
恒成立,
 ,
,
∴m<-1,
p∨q为真命题,p∧q为假命题,即p真q假,或p假q真,
如果p真q假,则有 ;
;
如果p假q真,则有 ;
;
所以实数m的取值范围为m<-1或m>5。
 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线, ,
,即命题q为真命题时,实数m的取值范围是m>5;
(2)若命题p真,即对任意实数x,不等式
 恒成立,
恒成立, ,
,∴m<-1,
p∨q为真命题,p∧q为假命题,即p真q假,或p假q真,
如果p真q假,则有
 ;
;如果p假q真,则有
 ;
;所以实数m的取值范围为m<-1或m>5。

练习册系列答案
相关题目
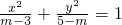 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.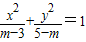 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.