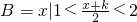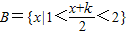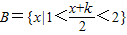题目内容
已知A={a|不等式x2+2ax+4>0在x∈R上恒成立},且B={x|1<
<2}
(1)若k=1,求A∩CRB;
(2)若CRA?CRB,求实数k的取值范围.
| x+k | 2 |
(1)若k=1,求A∩CRB;
(2)若CRA?CRB,求实数k的取值范围.
分析:(1)要求A∩CRB则需求出集合A,B而当k=1时B=(1,3)对于A={a|不等式x2+2ax+4>0在x∈R上恒成立}则相当于函数f(x)=x2+2ax+4的图象恒在x轴上方所对应的a的范围即A={a|4a2-16<0}然后利用交集的定义即可得解.
(2)在第一问的基础上求出集合A,B=(2-k,4-k)然后求出CRA,CRB再利用条件CRA?CRB即可求解.
(2)在第一问的基础上求出集合A,B=(2-k,4-k)然后求出CRA,CRB再利用条件CRA?CRB即可求解.
解答:解:(1)x2+2ax+4>0在R上恒成立
∴△=4a2-16<0
∴A=(-2,2)
又k=1时,B=(1,3)
∴CRB=(-∞,1]∪[3,+∞)
∴A∩CRB=(-2,1]
(2)∵B=(2-k,4-k)
由CRA?CRB可知B
A
∴
解不等式可得:2≤k≤4
∴△=4a2-16<0
∴A=(-2,2)
又k=1时,B=(1,3)
∴CRB=(-∞,1]∪[3,+∞)
∴A∩CRB=(-2,1]
(2)∵B=(2-k,4-k)
由CRA?CRB可知B
|
∴
|
解不等式可得:2≤k≤4
点评:本题主要考查了函数恒成立的问题以及集合间的运算和利用集合间的包含关系求参数范围.解题的关键是求出集合A而要求集合A则需明白x2+2ax+4>0在R上恒成立等价位对应的二次函数f(x)=x2+2ax+4的图象恒在x轴的上方也即△<0

练习册系列答案
相关题目