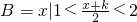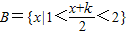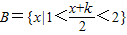题目内容
已知A={a|不等式x2+2ax+4>0在x∈R上恒成立},且B={x|1<
<2}
(1)若k=1,求A∩CRB;
(2)若CRA?CRB,求实数k的取值范围.
| x+k |
| 2 |
(1)若k=1,求A∩CRB;
(2)若CRA?CRB,求实数k的取值范围.
(1)x2+2ax+4>0在R上恒成立
∴△=4a2-16<0
∴A=(-2,2)
又k=1时,B=(1,3)
∴CRB=(-∞,1]∪[3,+∞)
∴A∩CRB=(-2,1]
(2)∵B=(2-k,4-k)
由CRA?CRB可知B
A
∴
解不等式可得:2≤k≤4
∴△=4a2-16<0
∴A=(-2,2)
又k=1时,B=(1,3)
∴CRB=(-∞,1]∪[3,+∞)
∴A∩CRB=(-2,1]
(2)∵B=(2-k,4-k)
由CRA?CRB可知B
|
∴
|
解不等式可得:2≤k≤4

练习册系列答案
相关题目