题目内容
在以下四个命题中，不正确的个数为（ ）
（1）若
与
-
都是非零向量，则
•
=
•
是
⊥(
-
)的充要条件
（2）已知不共线的三点A、B、C和平面ABC外任意一点O，点P在平面ABC内的充要条件是存在x，y，z∈R，
=x
+y
+z
且x+y+z=1
（3）空间三个向量
，
，
，若
∥
，
∥
， 则
∥
（4）对于任意空间任意两个向量
，
，
∥
的充要条件是存在唯一的实数λ，使
=λ
．
（1）若
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
（2）已知不共线的三点A、B、C和平面ABC外任意一点O，点P在平面ABC内的充要条件是存在x，y，z∈R，
| OP |
| OA |
| OB |
| OC |
（3）空间三个向量
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
（4）对于任意空间任意两个向量
| a |
| b |
| a |
| b |
| a |
| b |
分析：利用“两个向量垂直”等价于“两向量的数量积为零”知①正确；根据空间向量基本定理可以推得②正确，举反例可得③、④不正确，因此可得题中的正确命题有两个．
解答：解：对于（1），由向量垂直的充要条件得：
•
=
•
?
(
-
) =0?
⊥
-
，说明①正确．
对于（2），若
=x
+y
+z
且x+y+z=1，则
=(x-1)
+y
+z
=y(
-
)+z(
-
)
=y
+z
由空间向量基本定理，得
、
、
三个向量共面，说明点P在平面ABC内．
反之，如果点P在平面ABC内，类似地可以证明存在x，y，z∈R，
=x
+y
+z
且x+y+z=1，方法同上，因此②正确．
对于（3），若空间三个向量
，
，
，若
∥
且
∥
，但
是零向量，则不能满足
∥
，说明③不正确．
对于（4），若两个向量
，
，
∥
，但若
=
但
不是零向量，则不存在实数λ，使
=λ
成立说明④不正确．
故选B．
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
对于（2），若
| OP |
| OA |
| OB |
| OC |
| AP |
| OA |
| OB |
| OC |
| OB |
| OA |
| OC |
| OA |
=y
| AB |
| AC |
由空间向量基本定理，得
| AP |
| AB |
| AC |
反之，如果点P在平面ABC内，类似地可以证明存在x，y，z∈R，
| OP |
| OA |
| OB |
| OC |
对于（3），若空间三个向量
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| b |
| a |
| c |
对于（4），若两个向量
| a |
| b |
| a |
| b |
| b |
| o |
| a |
| a |
| b |
故选B．
点评：本题考查两个向量数量积的运算和充要条件的定义，属于基础题．熟练掌握向量运算性质，准确理解充要条件的含义，是解决本题的关键．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
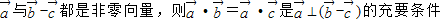
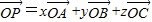且x+y+z=1
，若
，
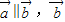
的充要条件是存在唯一的实数λ，使
．
且x+y+z=1
，若
，
的充要条件是存在唯一的实数λ，使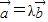
．