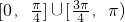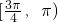题目内容
过曲线y=x2-2x+3上一点P作曲线的切线，若切点P的横坐标的取值范围是[1，
]，则切线的倾斜角的取值范围是（ ）
| 3 |
| 2 |
分析：求导函数，根据切点P的横坐标的取值范围，确定切线斜率的取值范围，从而可得切线的倾斜角的取值范围．
解答：解：求导函数可得，y′=2x-2
∵切点P的横坐标的取值范围是[1，
]，
∴2x-2∈[0，1]
设切线的倾斜角为α，则tanα∈[0，1]
∵α∈[0，π）
∴α∈[0，
]
故选B．
∵切点P的横坐标的取值范围是[1，
| 3 |
| 2 |
∴2x-2∈[0，1]
设切线的倾斜角为α，则tanα∈[0，1]
∵α∈[0，π）
∴α∈[0，
| π |
| 4 |
故选B．
点评：本题考查导数知识的运用，考查导数的几何意义，考查直线的倾斜角与斜率，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
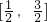，则切线的倾斜角的取值范围是
