题目内容
一袋中有x(x∈N*)个红球,3个黑球和2个白球,现从中任取2个球.(Ⅰ)当x=3时,求取出的2个球颜色都相同的事件的概率;
(Ⅱ)当x=3时,设ξ表示取出的2个球中红球的个数,求ξ的概率分布及数学期望;
(Ⅲ)如果取出的2个球颜色不相同的事件概率小于
 ,求x的最小值.
,求x的最小值.
【答案】分析:(Ⅰ)当x=3时袋中共有8个球,取出的2个球颜色都相同,则可能为2红、2黑、2白.代公式即可求得.
(Ⅱ)当x=3时,取出的2个球中红球的个数可能为0、1、2.求出相应的概率,即可求得分布列及期望.
(Ⅲ)取出的2个球颜色不相同,则可能为1红1黑、1红1白、1黑1白.使其概率和小于 ,求出最小的正整数x.
,求出最小的正整数x.
解答:解:(Ⅰ)当x=3时,设“取出的2个球颜色都相同”为事件A,
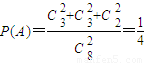 ,
,
答:取出的2球颜色都相同的事件概率为 .
.
(Ⅱ)当x=3时,ξ可取0、1、2,
∵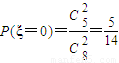 ,
,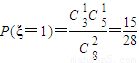 ,
,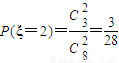
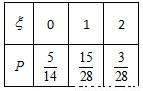
∴ξ的概率分布为:
ξ的数学期望为: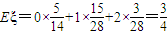 .
.
(Ⅲ)设“取出的2个球中颜色不相同”为事件B,
则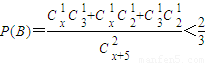 ,
,
∴x2-6x+2>0,
∴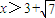 或
或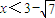 ,
,
∵x∈N
∴x的最小值为6.
点评:考查学生分析解决问题的能力,重点考查古典概型及计算公式.
(Ⅱ)当x=3时,取出的2个球中红球的个数可能为0、1、2.求出相应的概率,即可求得分布列及期望.
(Ⅲ)取出的2个球颜色不相同,则可能为1红1黑、1红1白、1黑1白.使其概率和小于
 ,求出最小的正整数x.
,求出最小的正整数x.解答:解:(Ⅰ)当x=3时,设“取出的2个球颜色都相同”为事件A,
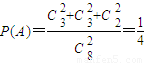 ,
,答:取出的2球颜色都相同的事件概率为
 .
.(Ⅱ)当x=3时,ξ可取0、1、2,
∵
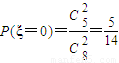 ,
,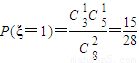 ,
,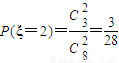
∴ξ的概率分布为:

ξ的数学期望为:
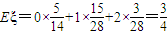 .
.(Ⅲ)设“取出的2个球中颜色不相同”为事件B,
则
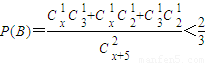 ,
,∴x2-6x+2>0,
∴
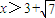 或
或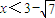 ,
,∵x∈N
∴x的最小值为6.
点评:考查学生分析解决问题的能力,重点考查古典概型及计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,求x的最小值.
,求x的最小值. ,求x的最小值.
,求x的最小值.