题目内容
已知logax+3logxa-logxy=3(a>1)(1)若设x=at,试用a、t表示y
(2)若y有最小值8,求a的值.
分析:对于(1)若设x=at,试用a、t表示y.首先对等式logax+3logxa-logxy=3利用换底公式化简为(logax)2-3logax+3=logay,然后把x=at代入化简即可.
对于(2)y有最小值8,求a的值.先根据(1)所解得的函数y=at2-3t+3,设z=t2-3t+3,然后根据复合函数求最值的方法求出y的最小值a
,得等式a
= 8,求解即可得到答案.
对于(2)y有最小值8,求a的值.先根据(1)所解得的函数y=at2-3t+3,设z=t2-3t+3,然后根据复合函数求最值的方法求出y的最小值a
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)已知 logax+3logxa-logxy=3即logax+3logxa-3=logxy利用换底公式有:logax+3logxa-3=
则;(logax)2-3logax+3=logay.
设x=at用则:t=logax.
即:t2-3t+3=logay,y=at2-3t+3.
故答案为y=at2-3t+3..
(2)当0<t≤2时,y有最小值8,
设z=t2-3t+3.则y=az,因为a>1所以函数y=az关于z单调递增.则z取最小值的时候y取最小值.
下求z的最小值,因为z=t2-3t+3,是开口向上的抛物线.则在对称轴取t=
得最小值z=
.代入函数y=az的最小值为y=a
.
因为y有最小值8,则a
= 8,a=16.
故答案为a=16.
| ||
|
则;(logax)2-3logax+3=logay.
设x=at用则:t=logax.
即:t2-3t+3=logay,y=at2-3t+3.
故答案为y=at2-3t+3..
(2)当0<t≤2时,y有最小值8,
设z=t2-3t+3.则y=az,因为a>1所以函数y=az关于z单调递增.则z取最小值的时候y取最小值.
下求z的最小值,因为z=t2-3t+3,是开口向上的抛物线.则在对称轴取t=
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
因为y有最小值8,则a
| 3 |
| 4 |
故答案为a=16.
点评:此题主要考查对数函数的运算问题,其中涉及到复合函数求最值的方法,在高考中属于重点考点,需要同学们理解并掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
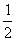 的值.
的值.