题目内容
若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1、x2总有以下不等式
≤f(
)成立,则称函数y=f(x)为区间D上的凸函数.
(1)证明:定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(2)设f(x)=ax2+x(a∈R,a≠0),并且x∈[0,1]时,f(x)≤1恒成立,求实数a的取值范围,并判断函数
f(x)=ax2+x(a∈R,a≠0)能否成为R上的凸函数;
(3)定义在整数集Z上的函数f(x)满足:①对任意的x,y∈Z,f(x+y)=f(x)f(y);②f(0)≠0,f(1)=2.
试求f(x)的解析式;并判断所求的函数f(x)是不是R上的凸函数说明理由.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
(1)证明:定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(2)设f(x)=ax2+x(a∈R,a≠0),并且x∈[0,1]时,f(x)≤1恒成立,求实数a的取值范围,并判断函数
f(x)=ax2+x(a∈R,a≠0)能否成为R上的凸函数;
(3)定义在整数集Z上的函数f(x)满足:①对任意的x,y∈Z,f(x+y)=f(x)f(y);②f(0)≠0,f(1)=2.
试求f(x)的解析式;并判断所求的函数f(x)是不是R上的凸函数说明理由.
分析:(1)利用作差法证明,即要证:
≤f(
),只要证:[f(x1)+f(x2)]-2f(
)≤0;
(2)首先根据自变量的范围进行分离常数,然后问题就转化为函数求最值的问题,求最值时利用配方法.根据a的范围和(1)判断是否为凸函数;
(3)首先令x=y=0,求出f(0)的值,在令y=-x,可得出f(x)与f(-x)之间的关系,反复利用这个关系数得出f(n)与f(1)的关系,就可得出f(x)的解析式,在利用基本不等式判断是否为凸函数.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
(2)首先根据自变量的范围进行分离常数,然后问题就转化为函数求最值的问题,求最值时利用配方法.根据a的范围和(1)判断是否为凸函数;
(3)首先令x=y=0,求出f(0)的值,在令y=-x,可得出f(x)与f(-x)之间的关系,反复利用这个关系数得出f(n)与f(1)的关系,就可得出f(x)的解析式,在利用基本不等式判断是否为凸函数.
解答:解:(1)证明:对任意x1,x2∈R,当a<0,
有[f(x1)+f(x2)]-2f(
)=ax12+bx1+c+ax22+bx2+c-2[a(
)2+b(
)+c]=ax12+ax22-
a(x12+x22+2x1x2)=
a(x1-x2)2 (3分)
∴当a<0时,f(x1)+f(x2)≤2f(
),即
≤f(
)
当a<0时,函数f(x)是凸函数. (5分)
(2)当x=0时,对于a∈R,有f(x)≤1恒成立;当x∈(0,1]时,要f(x)≤1恒成立,即ax2≤-x+1,
∴a≤
-
=(
-
)2-
恒成立,∵x∈(0,1],∴
≥1,当
=1时,(
-
)2-
取到最小值为0,
∴a≤0,又a≠0,∴a的取值范围是(-∞,0).
由此可知,满足条件的实数a的取值恒为负数,由(1)可知函数f(x)是凸函数 (11分)
(3)令x=y=0,则f(0)=[f(0)]2,∵f(0)≠0,∴f(0)=1,(12分)
令y=-x,则1=f(0)=f(x-x)=f(x)f(-x),故f(x)=
;
若n∈N*,则f(n)=f[(n-1)+1]=f(n-1)f(1)=2f(n-1)=…=[f(1)]2; (14分)
若n<0,n∈Z,则-n∈N*,∴f(n)=
=
=2n;∴x∈Z时,f(x)=2x.
综上所述,对任意的x∈Z,都有f(x)=2x; (15分)
∵
[20+21]=
>
,所以f(x)不是R上的凸函数. (16分)
(对任意x1,x2∈R,有
[f(x1)+f(x2)]=
[2x1+2x2]≥
×2
=f(
),所以f(x)不是R上的凸函数. 16分)
有[f(x1)+f(x2)]-2f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当a<0时,f(x1)+f(x2)≤2f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
当a<0时,函数f(x)是凸函数. (5分)
(2)当x=0时,对于a∈R,有f(x)≤1恒成立;当x∈(0,1]时,要f(x)≤1恒成立,即ax2≤-x+1,
∴a≤
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
∴a≤0,又a≠0,∴a的取值范围是(-∞,0).
由此可知,满足条件的实数a的取值恒为负数,由(1)可知函数f(x)是凸函数 (11分)
(3)令x=y=0,则f(0)=[f(0)]2,∵f(0)≠0,∴f(0)=1,(12分)
令y=-x,则1=f(0)=f(x-x)=f(x)f(-x),故f(x)=
| 1 |
| f(-x) |
若n∈N*,则f(n)=f[(n-1)+1]=f(n-1)f(1)=2f(n-1)=…=[f(1)]2; (14分)
若n<0,n∈Z,则-n∈N*,∴f(n)=
| 1 |
| f(-n) |
| 1 |
| 2-n |
综上所述,对任意的x∈Z,都有f(x)=2x; (15分)
∵
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
(对任意x1,x2∈R,有
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2x1+x2 |
| x1+x2 |
| 2 |
点评:本题给出了数学新定义凸函数,在判断一个函数是凸函数要根据定义,方法是“作差法”,本题的第一问与第二问紧密联系解题是要抓住这一点.难点在第三问,怎样给x,y赋值,怎样利用好①和②,最终求出解析式.

练习册系列答案
相关题目

 的单调性;
的单调性;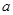 的取值范围;
的取值范围;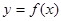 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式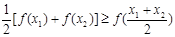 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数 ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.