Question

已知AB是经过抛物线y²=2px（p＞0）的焦点F且与两坐标轴不垂直的一条弦，点M（-1，0）满足∠AMF=∠BMF，则p的值是（　　）

• A、1
• B、2
• C、4
• D、2或4

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：由题意画出图象作AC⊥x轴、BD⊥x轴，设AB的直线方程y=k（x-

p

2

）（k≠0），A（x₁，y₁）、B（x₂，y₂），联立直线方程和抛物线方程消去y，由韦达定理求出x₁+x₂和x₁x₂式子，由∠AMF=∠BMF得tan∠AMF=tan∠BMF，由图象得

AC

MC

=

BD

MD

，用A、B的坐标表示出线段的长，把求出的式子代入化简，列出关于p的方程再化简求值．

解答： 解：如右图作AC⊥x轴，BD⊥x轴，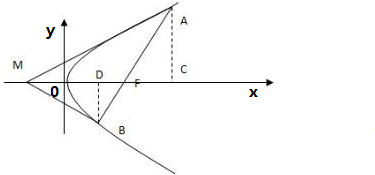
由题意得设AB的直线方程为：y=k（x-

p

2

）（k≠0），A（x₁，y₁），B（x₂，y₂），
由

y=k(x- p 2 ) y2=2px

得，k2x2-(k2p+2p)x+

k2p2

4

=0，
则x₁+x₂=

k2p+2p

k2

，x₁x₂=

p2

4

，
因为∠AMF=∠BMF，所以tan∠AMF=tan∠BMF，即

AC

MC

=

BD

MD

，
不妨设x₁＞

p

2

，x₂＜

p

2

，
则AC=|y₁|=|k（x₁-

p

2

）|=|k|（x₁-

p

2

），BD=|y₂|=|k（x₂-

p

2

）|=|k|（

p

2

-x₂），
且MC=x₁，+1，MD=x₂，+1，
代入

AC

MC

=

BD

MD

得，

|k|(x1- p 2 )

x1+1

=

|k|( p 2 -x2)

x2+1

，
化简得，2x₁x₂+（x₁+x₂）（1-

p

2

）-p=0，
则2×

p2

4

+

k2p+2p

k2

（1-

p

2

）-p=0，化简得

2-p

k2

=0，
因为k≠0，所以p=2，
故选：B．

点评：本题考查直线与抛物线的关系，一元二次方程的根与系数的关系，考查化简计算能力，是中档题．