题目内容
已知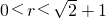 ,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是
- A.外切
- B.外离
- C.相交
- D.内含
C
分析:根据两圆的标准方程,求出圆心和半径,再求得两圆的圆心距d=|CA|的值,再由两圆的圆心距大于两圆的半径之差,
且小于两圆的半径之和,从而判断圆相交.
解答:由于两圆x2+y2=r2与的圆心O(0,0)半径为r,圆(x-1)2+(y+1)2=2的圆心为A(1,-1),半径等于 ,
,
故两圆的圆心距d=|CA|= .
.
∵已知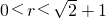 ,显然,|r-
,显然,|r- |<d<r+
|<d<r+ ,即两圆的圆心距大于两圆的半径之差,且小于两圆的半径之和,
,即两圆的圆心距大于两圆的半径之差,且小于两圆的半径之和,
故两圆相交,
故选C.
点评:本题主要考查圆的标准方程的特征,两圆的位置关系的判断方法,属于中档题.
分析:根据两圆的标准方程,求出圆心和半径,再求得两圆的圆心距d=|CA|的值,再由两圆的圆心距大于两圆的半径之差,
且小于两圆的半径之和,从而判断圆相交.
解答:由于两圆x2+y2=r2与的圆心O(0,0)半径为r,圆(x-1)2+(y+1)2=2的圆心为A(1,-1),半径等于
 ,
,故两圆的圆心距d=|CA|=
 .
.∵已知
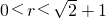 ,显然,|r-
,显然,|r- |<d<r+
|<d<r+ ,即两圆的圆心距大于两圆的半径之差,且小于两圆的半径之和,
,即两圆的圆心距大于两圆的半径之差,且小于两圆的半径之和,故两圆相交,
故选C.
点评:本题主要考查圆的标准方程的特征,两圆的位置关系的判断方法,属于中档题.

练习册系列答案
相关题目
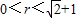 ,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )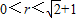 ,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )