题目内容
已知C(1,0),O为坐标原点,过双曲线![]() 的右焦点F的直线与双曲线相交于A、B两点。
的右焦点F的直线与双曲线相交于A、B两点。
(1)求![]() 的值;
的值;
(2)若动点M满足![]() ,求点M的轨迹方程。
,求点M的轨迹方程。
解:(I)当AB与x轴垂直时,点A、B的坐标分别为(2,、![]() )、(2,
)、(2,![]() ),
),
此时![]() =(1,
=(1,![]() )?(1,
)?(1,![]() )=-1
)=-1
当AB不与x轴垂直时,设直线AB的方程是y=k(x--2)(k≠±1)
代人X2-y2=2,有(1--k2)x2+4k2x-(4k2+2)=0.
设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,
所以![]() ,
,
于是![]()
![]()
![]()
![]() .
.
综上所述,![]() -1.
-1.
(Ⅱ)设M(x,y),则![]() =(x-1,y),
=(x-1,y),![]()
![]()
由![]() 得:
得:
 (以下分两种解法)
(以下分两种解法)
解法一:于是AB的中点坐标为![]() .
.
当AB不与x轴垂直时,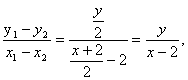
即![]()
又因为A,B两点在双曲线上,所以![]() ,两式相减得
,两式相减得
(x1一x2)(x1+ x2)=(y1-y2)(y1+y2),即(x1一x2)(x+2)=(y1-y2)y.
将![]() 代入上式,化简得x2-y2=4
代入上式,化简得x2-y2=4
当AB与x轴垂直时,x1=x2=2,求得M(2,0),也满足上述方程.
所以点M的轨迹方程是x2一y2=4
解法二:当AB不与x轴垂直时,由(I)可知:
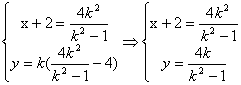
消去参数k得:x2一y2=4
当AB与x轴垂直时,x1=x2=2,yl+y2=0,求得M(2,0),也满上述方程
所以点M的轨迹方程是x2-y2=4.

练习册系列答案
相关题目
 (2009•湖北模拟)已知A(-1,0)、B(3,0),M、N是圆O:x2+y2=1上的两个动点,且M、N关于x轴对称,直线AM与BN交于P点.
(2009•湖北模拟)已知A(-1,0)、B(3,0),M、N是圆O:x2+y2=1上的两个动点,且M、N关于x轴对称,直线AM与BN交于P点.