题目内容
当x∈（0，+∞）时，幂函数y=（m2-m-1）x-5m-3为减函数，则实数m的值为
- A.m=2
- B.m=-1
- C.m=-1或m=2
- D.m≠
A
分析：根据给出的函数为幂函数，由幂函数概念知m2-m-1=1，再根据函数在（0，+∞）上为减函数，得到幂指数应该小于0，求得的m值应满足以上两条．
解答：因为函数y=（m2-m-1）x-5m-3既是幂函数又是（0，+∞）的减函数，
所以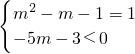
解得：m=2．
故选A．
点评：本题考查了幂函数的概念及性质，解答此题的关键是掌握幂函数的定义，此题极易把系数理解为不等于0而出错，属基础题．
分析：根据给出的函数为幂函数，由幂函数概念知m2-m-1=1，再根据函数在（0，+∞）上为减函数，得到幂指数应该小于0，求得的m值应满足以上两条．
解答：因为函数y=（m2-m-1）x-5m-3既是幂函数又是（0，+∞）的减函数，
所以
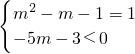解得：m=2．故选A．
点评：本题考查了幂函数的概念及性质，解答此题的关键是掌握幂函数的定义，此题极易把系数理解为不等于0而出错，属基础题．
练习册系列答案
相关题目
函数f（x）是R上以2为周期的奇函数，已知当x∈（0，1）时，f（x）=log2
，则f（x）在区间（1，2）上是（ ）
| 1 |
| 1-x |
| A、减函数，且f（x）＜0 |
| B、增函数，且f（x）＜0 |
| C、减函数，且f（x）＞0 |
| D、增函数，且f（x）＞0 |